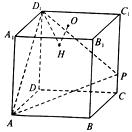
21．(14分)如图，在棱长为4的正方体ABCD-A₁B₁C₁D₁中，O是正方形A₁B₁C₁D₁的中心，点P在棱CC₁上，且CC₁ = 4CP.

(1)求直线AP与平面BCC₁B₁所成角的大小；(结果用反三角函数值表示)

(2)设O点在平面D₁AP上的射影是H，求证：D₁H⊥AP；

(3)求点P到平面ABD₁的距离.

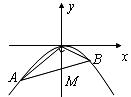
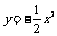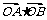20．(13分)抛物线上有两点A (x₁, y₁)，B (x₂, y₂)，且= 0，又知点M (0, –2). (1)求证：A、M、B三点共线； (2)若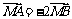，求AB所在的直线方程.

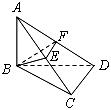
19．(12分)已知三棱锥A-BCD的侧棱AB⊥底面BCD，BC = CD，∠BCD = 90°，∠ADB = 30°，E、F分别是侧棱AC、AD的中点.

(1)求证：平面BEF⊥平面ABC；(2)求平面BEF和平面BCD所成的角.

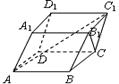
18．(12分)在平行六面体ABCD-A₁B₁C₁D₁中，AB = AD = AA₁= 1，∠A₁AB =∠A₁AD =∠DAB = 60°.

(1)求对角线AC_­1的长；(2)求异面直线AC₁与B₁C的夹角.

17．(12分)△ABC的两个顶点A、B的坐标分别是(–6, 0)，(6, 0)，边AC、BC所在直线的斜率之积等于常数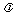(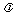≠0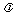，∈R)，讨论顶点C的轨迹是什么？

16．(12分)如图，在直三棱柱ABC-A₁B₁C₁中，∠ACB = 90°，点D是AB的中点.

(1)求证：AC⊥BC_­1；

(2)求证：AC₁∥平面CDB_­1.

15．已知正三棱柱ABC-A₁B₁C₁的各棱长相等，M是BB₁的中点，则面AC₁M与面ABC成的锐二面角是　　　　　　　　　　　　 .

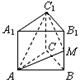
14．正四面体A-BCD的棱长为1，则A到底面BCD的距离为　　　　　 .

13．方程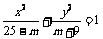表示焦点在y轴上的椭圆，则m的取值范围是　　　　　　　　　　　 .

12．过抛物线y² = 8x的焦点，倾斜角为45°的直线的方程是　　　　　　　　　　　　　　 .