
2.从甲,乙,丙三人中任选两名代表,甲被选中的概率( )
A.1/2 B.1/3 C.2/3 D.1
1.某人忘记了电话号码的最后一个数字,随意拨号,则拨号不超过三次而接通电话的概率为( )
A.9/10 B.3/10 C.1/8 D.1/10
22.(本小题满分14分)
已知函数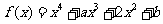 (
(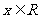 ),其中
),其中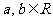 .
.
(Ⅰ)当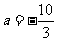 时,讨论函数
时,讨论函数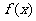 的单调性;
的单调性;
(Ⅱ)若函数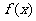 仅在
仅在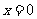 处有极值,求
处有极值,求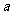 的取值范围;
的取值范围;
(Ⅲ)若对于任意的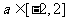 ,不等式
,不等式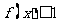 在
在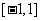 上恒成立,求
上恒成立,求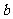 的取值范围.
的取值范围.
21.在直角坐标系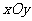 中,点P到两点
中,点P到两点 ,
,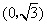 的距离之和等于4,设点P的轨迹为
的距离之和等于4,设点P的轨迹为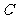 ,直线
,直线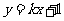 与C交于A,B两点.
与C交于A,B两点.
(Ⅰ)写出C的方程;
(Ⅱ)若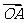
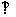
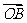 ,求k的值;
,求k的值;
(Ⅲ)若点A在第一象限,证明:当k>0时,恒有|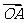 |>|
|>|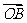 |.
|.
20.(本小题满分12分)
在数列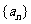 中,
中,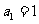 ,
,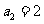 ,且
,且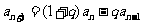 (
(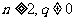 ).
).
(Ⅰ)设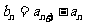 (
(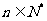 ),证明
),证明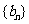 是等比数列;
是等比数列;
(Ⅱ)求数列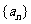 的通项公式;
的通项公式;
19.如图,在三棱锥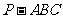 中,
中,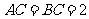 ,
,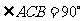 ,
,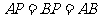 ,
,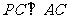 .
.
(Ⅰ)求证: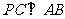 ;
;
(Ⅱ)求二面角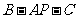 的大小;
的大小;
(Ⅲ)求点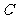 到平面
到平面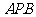 的距离.
的距离.

17(本小题满分12分)
已知函数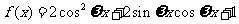 (
(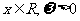 )的最小值正周期是
)的最小值正周期是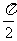 .
.
(Ⅰ)求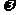 的值;
的值;
(Ⅱ)求函数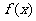 的最大值,并且求使
的最大值,并且求使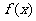 取得最大值的
取得最大值的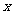 的集合.
的集合.
18.(本小题共13分)
甲、乙等五名奥运志愿者被随机地分到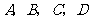 四个不同的岗位服务,每个岗位至少有一名志愿者.
四个不同的岗位服务,每个岗位至少有一名志愿者.
(Ⅰ)求甲、乙两人同时参加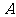 岗位服务的概率;
岗位服务的概率;
(Ⅱ)求甲、乙两人不在同一个岗位服务的概率;
(Ⅲ)设随机变量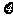 为这五名志愿者中参加
为这五名志愿者中参加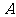 岗位服务的人数,求
岗位服务的人数,求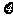 的分布列.
的分布列.
16.某地奥运火炬接力传递路线共分6段,传递活动分别由6名火炬手完成.如果第一棒火炬手只能从甲、乙、丙三人中产生,最后一棒火炬手只能从甲、乙两人中产生,则不同的传递方案共有 种.(用数字作答).
15.已知随机变量 服从正态分布N(3,a2),则P(
服从正态分布N(3,a2),则P(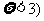 =
。
=
。
14.
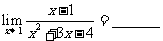 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com