
4.从某鱼池中捕得120条鱼,做了记号之后,再放回池中,经过适当的时间后,再从池中捕得100条鱼,计算其中有记号的鱼为10条,试估计鱼池中共有鱼的条数为( )
A. 1000 B. 1200 C. 130 D.1300
3.对总数为N的一批零件抽取一个容量为30的样本,若每个零件被抽到的概率为0.25,则N的值为( )
A.120 B.200 C.150 D.100
2.某次考试有70000名学生参加,为了了解这70000名考生的数学成绩,从中抽取1000名考生的数学成绩进行统计分析,在这个问题中,有以下四种说法:
①1000名考生是总体的一个样本;②1000名考生数学成绩的平均数是总体平均数;
③70000名考生是总体; ④样本容量是1000,
其中正确的说法有:( )
A.1种 B.2种 C.3种 D.4种
1.为了了解全校900名高一学生的身高情况,从中抽取90名学生进行测量,下列说法正确的是( )
A.总体是900 B.个体是每个学生 C.样本是90名学生 D.样本容量是90
22.(本小题满分12分)
已知函数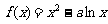 在
在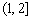 是增函数,
是增函数,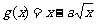 在(0,1)为减函数.
在(0,1)为减函数.
(I)求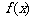 、
、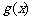 的表达式;
的表达式;
(II)求证:当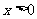 时,方程
时,方程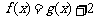 有唯一解;
有唯一解;
(III)当 时,若
时,若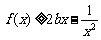 在
在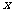 ∈
∈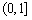 内恒成立,求
内恒成立,求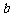 的取值范围.
的取值范围.
21.已知函数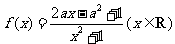 ,其中
,其中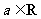 .
.
(Ⅰ)当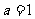 时,求曲线
时,求曲线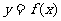 在点
在点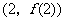 处的切线方程;
处的切线方程;
(Ⅱ)当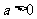 时,求函数
时,求函数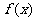 的单调区间与极值.
的单调区间与极值.
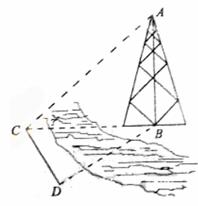
20.如下图,测量河对岸的塔高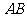 时,可以选与塔底
时,可以选与塔底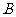 在同一水平面内的两个测点
在同一水平面内的两个测点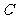 与
与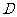 .现测得
.现测得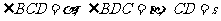 ,并在点
,并在点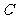 测得塔顶
测得塔顶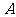 的仰角为
的仰角为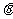 ,求塔高
,求塔高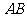 .
.
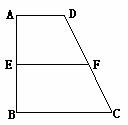
19.(本小题满分12分)
已知梯形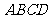 中,
中,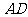 ∥
∥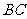 ,
,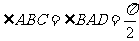 ,
, 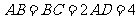 ,
,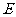 、
、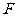 分别是
分别是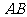 、
、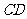 上的点,
上的点,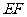 ∥
∥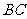 ,
,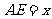 ,
,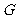 是
是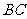 的中点。沿
的中点。沿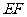 将梯形
将梯形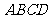
翻折,使平面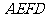 ⊥平面
⊥平面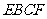 (如图) .
(如图) .
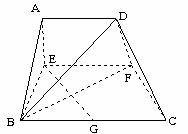
(Ⅰ) 当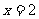 时,求证:
时,求证: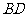 ⊥
⊥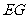 ;
;
(Ⅱ) 若以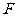 、
、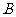 、
、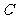 、
、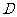 为顶点的三棱锥的体积记为
为顶点的三棱锥的体积记为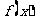 ,求
,求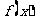 的最大值;
的最大值;
(Ⅲ) (理)当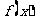 取得最大值时,求二面角
取得最大值时,求二面角 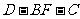 的余弦值.
的余弦值.
18.(本小题满分12分)
已知函数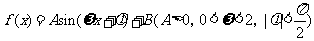 的一系列对应值如下表:
的一系列对应值如下表:
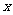
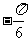
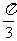
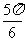
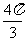
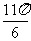
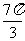
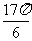
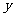
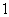
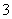
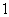
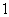
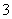
(Ⅰ)根据表格提供的数据求函数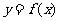 的解析式;
的解析式;
(II)当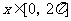 时,求方程
时,求方程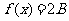 的解.
的解.
17.(本小题满分12分)
已知命题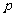 :对
:对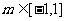 ,不等式
,不等式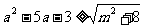 恒成立;命题
恒成立;命题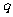 :不等式
:不等式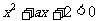 有解;若
有解;若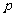 是真命题,
是真命题,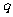 是假命题,求
是假命题,求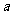 的取值范围.
的取值范围.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com