
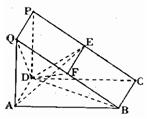
19.(本小题满分12分)如图:ABCD为正方形,ADPQ也是正方形,PD⊥平面AC,E、F依次分别为PC、BQ的中点。
(1)证明:平面DEF⊥平面BDQ;
(2)求直线AE与平面BDQ所成角的余弦值。
18.(本小题满分12分)已知△ABC的三个内角A、B、C成等差数列,其外接圆半径为1,且有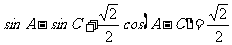 。
。
(1)求A、B、C的大小;
(2)求△ABC的面积。
17.(本小题满分12分)甲、乙两支蓝球队进行比赛,已知每一场甲队获胜的概率为0.6,乙队获胜的概率为0.4,每场比赛均要分出胜负,比赛时采用三场两胜制,即先取得两场胜利的球队胜出。
(1)求甲队以二比一获胜的概率;
(2)求乙队获胜的概率。
16.某校高二年级有8个班,其中3个文科班。现安排4名数学老师承担该年级数学课教学任务,每人2个班。如果有1名老师同时承担了2个文科班的教学工作,那么不同的排课方案有 种(用数字作答)
15.已知一个球与一个二面角的两个半平面都相切,若球心到二面角的棱的距离是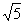 ,切点到二面角棱的距离是1,则球的体积是
。
,切点到二面角棱的距离是1,则球的体积是
。
14.已知实数x,y满足线性约束条件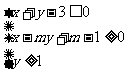 ,若目标函数
,若目标函数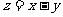 的最小值为
的最小值为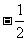 ,则实数m=
。
,则实数m=
。
13.已知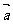 与
与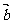 均为单位向量,它们的夹角为60°,那么
均为单位向量,它们的夹角为60°,那么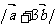 等于
。
等于
。
12.定义:一个没有重复数字的n位正整数(n≥3,n∈N*),各数位上的数字从左到右依次成等差数列,我们就称这个数为期望数。则由1,2,3,4,5,6,7构成三位数中期望数出现的概率为 ( )
A.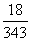 B.
B.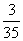 C.
C.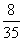 D.
D.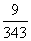
11.设O是△ABC的外心,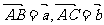 ,且
,且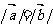 则
则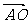 可用
可用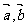 表示为 ( )
表示为 ( )
A.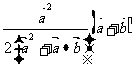 B.
B.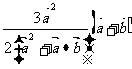
C.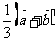 D.
D.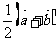
10.直线y=x+b与圆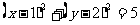 有公共点的一个充分不必要条件为 ( )
有公共点的一个充分不必要条件为 ( )
A.b≤4 B.b≥0 C.-4≤b≤4 D.0≤b≤4
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com