
1.设全集为R,集合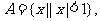 集合
集合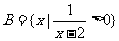 ,则有 ( )
,则有 ( )
A.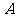
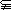
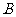 B.
B.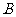
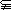
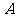 C.
C.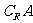
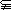
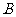 D.
D.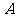
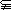
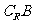
22.(本大题满分14分)
已知数列
(1)令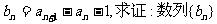 是等比数列;
是等比数列;
(2)求数列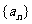 的通项
的通项
(3)设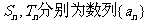 、
、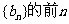 项和,是否存在实数
项和,是否存在实数
为等差数列?若存在,试求出λ,若不存在,请证明理由。
21.(本大题满分12分)
如图,椭圆两焦点F1、F2与短轴两端点B1、B2正好是正方形的四个顶点,且焦点到椭圆上一点最近的距离为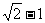 。
。
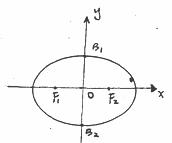
(1)求椭圆的标准方程;
(2)过点D(0,2)的直线与椭圆交于不同的两点M、N,且M在D、N之间,设
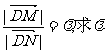 的取值范围。
的取值范围。
20.(本大题满分12分)
已知函数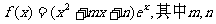 为常数。
为常数。
(1)若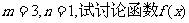 的单调性;
的单调性;
(2)若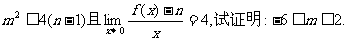
19.(本大题满分12分)
如图,四面体ABCD中,O、E分别是BD、BC的中点,CA=CB=CD=BD=2,AD=AB=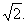
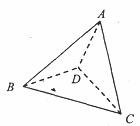
(1)求证:AO⊥平面BCD;
(2)求异面直线AB与CD所成角的大小;
(3)求点E到平面ACD的距离。
18.(本小题满分12分)
口袋里装有大小相同的4个红球和8个白球,甲、乙两人依规则从袋中有放回摸球,每次摸出一个球,规则如下:若一方摸出一个红球,则此人继续下一次摸球;若一方摸出一个白球,则由对方接替下一次摸球,且每次摸球彼此相互独立,并由甲进行第一次摸球。
(I)求在前三次摸球中,甲摸得红球的次数ξ的数学期望。
(II)设第n次由甲摸球的概率为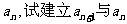 的递推关系,并求数列
的递推关系,并求数列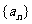 的通项公式。
的通项公式。
17.(本大题满分12分)
在△ABC中,角A、B、C的对边分别为a,b,c,且满足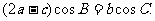
(1)求角B的大小;
(2)设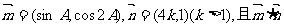 的最大值为7,求k的值。
的最大值为7,求k的值。
16.已知B地在A地的正东方向4km处,C地在B地的北偏东30°方向2km处,河流的沿岸PQ(曲线)上任意一点到A的距离比到B的距离远2km,现要在曲线PQ上选一处M建一码头,向B、C两地转运货物。经测算,以M到B、C修建公路的费用分别为a万元/km,2a万元/km,那么修建这两条公路的总费用最低是 万元。
15.已知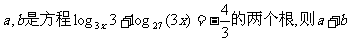 =
。
=
。
14.函数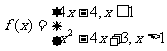 的图像和函数
的图像和函数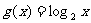 的图像的交点个数为
的图像的交点个数为
。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com