
20.(本小题满分12分)
已知椭圆C的中心在原点,焦点在x轴上,它的一个顶点恰好是抛物线y=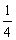 x2的焦点,离心率等于
x2的焦点,离心率等于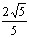 .
.
(1)求椭圆C的方程;
(2)过椭圆C的右焦点F作直线l交椭圆C于A、B两点,交y轴于M点,若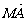 =λ1
=λ1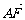 ,
,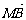 =λ2
=λ2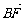 ,求证λ1+λ2为定值.
,求证λ1+λ2为定值.
19.(本小题满分14分)
已知数列{an}中,an=2-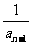 ( n≥2,n∈N+)
( n≥2,n∈N+)
(1)若a1=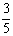 ,数列{bn}满足bn=
,数列{bn}满足bn=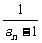 ( n∈N+),求证数列{bn}是等差数列;
( n∈N+),求证数列{bn}是等差数列;
(2)若a1=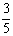 ,求数列{an}中的最大项与最小项,并说明理由.
,求数列{an}中的最大项与最小项,并说明理由.
18.(本小题满分14分)
如图,正三棱柱ABC-A1B1C1的底面边长是2,D是侧棱CC1的中点,直线AD与侧面BB1C1C所成的角为45°.
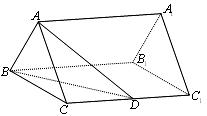
(1)求此正三棱柱的侧棱长;
(2)求二面角A-BD-C的大小;
(3)求点C到平面ABD的距离.
17.(本小题满分13分)
某校设计了一个实验学科的实验考查方案:考生从6道备选题中一次性随机抽取3题,按照题目要求独立完成全部实验操作.规定:至少正确完成其中2题的便可提高通过.已知6道备选题中考生甲有4题能正确完成,2题不能完成;考生乙每题正确完成的概率都是,且每题正确完成与否互不影响.求:
(1)考生甲通过实验考查的概率;
(2)考生乙通过实验考查的概率;
(3) 甲、乙两考生至少有一人通过实验考查的概率.
16.(本小题满分12分)
设函数f(x)=2cosx(cosx+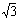 sinx)-1,x∈R
sinx)-1,x∈R
(1)求f(x)的最小正周期T;
(2)求f(x)的单调递增区间.
15.已知函数f (x)=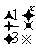 -log2x正实数a、b、c成公差为正数的等差数列,且满足f (a) f (b)f (c)<0,若实数d是方程f (x)=0的一个解,那么下列四个判断:
-log2x正实数a、b、c成公差为正数的等差数列,且满足f (a) f (b)f (c)<0,若实数d是方程f (x)=0的一个解,那么下列四个判断:
① d<a; ②d>b; ③d<c; ④d>c中有可能成立的为 (填序号).
14.已知Sn是数列{an}的前n项和,a2 =5, an+1=2 an-1, 则S4= ;
13.已知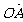 =(k, 12),
=(k, 12),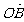 =(4, 5),
=(4, 5),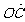 =(-k, 10),且A、B、C三点共线,则k=
;
=(-k, 10),且A、B、C三点共线,则k=
;
12.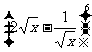 的展开式的中间项为
;
的展开式的中间项为
;
11.已知集合P={x|5x-a≤0}, Q={x|6x-b>0},a, b∈N, 且A∩B∩N={2,3,4},则整数对(a, b)的个数为
A.56 B.42 C.30 D.20
第Ⅱ卷(非选择题, 共95分)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com