
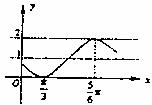
8.函数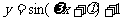 的一段图象如图所示,则它的最小正周期T及
的一段图象如图所示,则它的最小正周期T及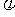 依次为( )
依次为( )
A.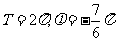 B.
B.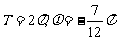
C.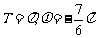 D.
D.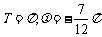
7.在△ABC中,已知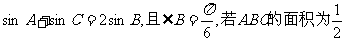 ,则∠B的对边b等于 ( )
,则∠B的对边b等于 ( )
A.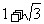 B.3+
B.3+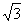 C.2+
C.2+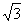 D.
D.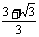
6.已知抛物线
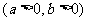 有相同的焦点F,点A是两曲线的交点,且AF⊥x轴,则双曲线的离心率为 ( )
有相同的焦点F,点A是两曲线的交点,且AF⊥x轴,则双曲线的离心率为 ( )
A.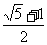 B.
B.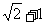 C.
C.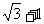 D.
D.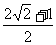
5.已知等比数列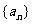 的前n项和为Sn,且S3=3a1,则数列
的前n项和为Sn,且S3=3a1,则数列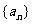 的公比q的值为
( )
的公比q的值为
( )
A.-2 B.1
C.-1或2 D.1或-2
4.在下图的程度框图中,输出的s的值为( )
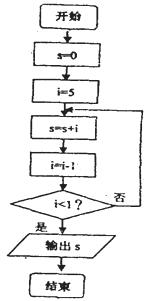
A.12 B.14
C.15 D.20
3.已知命题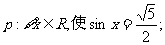
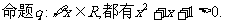 给出下列结论:
给出下列结论:
①命题“ ”是真命题 ②命题“
”是真命题 ②命题“ ”是假命题
”是假命题
③命题“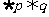 ”是真命题; ④命题“
”是真命题; ④命题“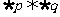 ”是假命题
”是假命题
其中正确的是 ( )
A.②④ B.②③ C.③④ D.①②③
2.已知R为实数集,集合M=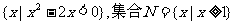 ,则
,则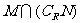 =( )
=( )
A.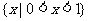 B.
B.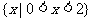
C.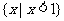 D.
D.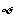
1.已知i是虚数单位,复数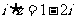 ,则复数z的对应点位于 ( )
,则复数z的对应点位于 ( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
21.(本小题满分13分)已知函数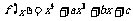
(1)若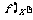 在
在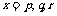 处取得极值,其中
处取得极值,其中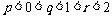 ,求实数a的取值范围;
,求实数a的取值范围;
(2)在(1)的条件下,若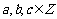 ,且
,且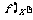 =0有4个不等的实数解,求
=0有4个不等的实数解,求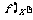 的解析式。
的解析式。
20.(本小题满分13分)已知数列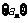 是首项为1,公差为2的等差数列,对每一个
是首项为1,公差为2的等差数列,对每一个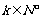 ,在
,在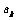 与
与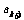 之间插入
之间插入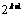 个2,得到新数列
个2,得到新数列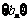 ,设
,设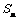 与
与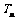 分别是数列
分别是数列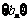 和数列
和数列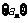 的前n项和。
的前n项和。
(1)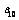 是数列
是数列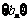 的第几项;
的第几项;
(2)是否存在正整数m,使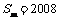 ?若存在,求出m 的值,若不存在,请说明理由;
?若存在,求出m 的值,若不存在,请说明理由;
(3)若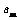 是数列
是数列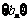 的
的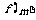 项,试比较
项,试比较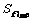 与
与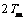 的大小,并说明理由。
的大小,并说明理由。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com