
(13)不等式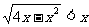 的解集是 .
的解集是 .
(14)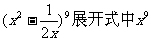 的系数是
.
的系数是
.
(15)在平面几何里,有勾股定理:“设△ABC的两边AB,AC互相垂直,则AB2+AC2=BC2” 拓展到空间,类比平面几何的勾股定理,研究三棱锥的侧面面积与底面面积间的关系,可以得出的正确结论是:“设三棱锥A-BCD的三个侧面ABC、ACD、ADB两两相互垂直,则 .”
(16)一个地区分为5个行政区域,现给地图着色,要求相邻区域不得使用同一颜色,现有4种颜色可供选择,则不同的着色方法共有 种.(以数字作答)
(1)直线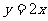 关于x轴对称的直线方程为
关于x轴对称的直线方程为
(A)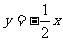 (B)
(B)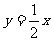 (C)
(C)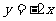 (D)
(D)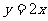
(2)已知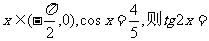
(A)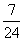 (B)-
(B)-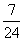 (C)
(C)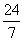 (D)-
(D)-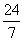
(3)抛物线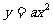 的准线方程是
的准线方程是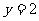 ,则a的值为
,则a的值为
(A)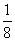 (B)-
(B)-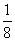 (C)8 (D)-8
(C)8 (D)-8
(4)等差数列{a n}中,已知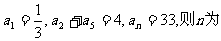
(A)48 (B)49 (C)50 (D)51
(5)双曲线虚轴的一个端点为M,两个焦点为F1,F2,F1MF2=120°则双曲线的离心率为
(A)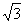 (B)
(B)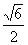 (C)
(C)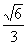 (D)
(D)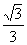
(6)设函数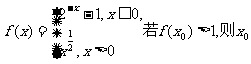 的取值范围是
的取值范围是
(A)(-1,1) (B)(-1,+∞)
(C)(-∞,-2)∪(0,+∞) (D)(-∞,-1)∪(1,+∞)
(7)已知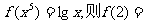
(A)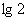 (B)
(B)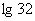 (C)
(C)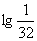 (D)
(D)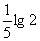
(8)函数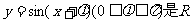 上的偶函数,则
上的偶函数,则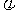 =
=
(A)0 (B)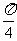 (C)
(C)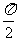 (D)
(D)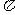
(9)已知点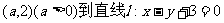 的距离为1,则a=
的距离为1,则a=
(A)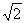 (B)-
(B)-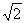 (C)
(C)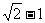 (D)
(D)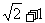
(10)已知圆锥的底面半径为R,高为3R,它的内接圆柱的底面半径为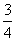 R,该圆柱的全面积为
R,该圆柱的全面积为
(A)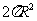 (B)
(B)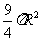 (C)
(C)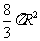 (D)
(D)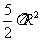
(11)已知长方形的四个顶点A(0,0),B(2,0),C(2,1)和D(0,1)一质点从AB的中点P0沿与AB夹角为θ的方向射到BC上的点P1后,依次反射到CD、DA和AB上的点P2、P3和P4(入射角等于反射角).若P4与P0重合,则tgθ=
(A)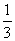 (B)
(B)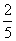 (C)
(C)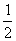 (D)1
(D)1
(12)一个四面体的所有棱长都为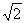 ,四个顶点在同一球面上,则此球的表面积为
,四个顶点在同一球面上,则此球的表面积为
(A)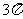 (B)4
(B)4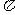 (C)
(C)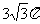 (D)
(D)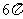
(17)(本小题满分12分)
已知复数z的辐角为60°,且| z-1 |是| z |和| z-2 |的等比中项,求| z |.
(18)(本小题满分12分)
如图,在直三棱柱ABC-A1B1C1中,底面是等腰直角三角形,∠ACB=90°.侧棱AA1=2,D、E分别CC1与A1B的中点,点E在平面ABD上的射影是△ABD的重心G.

(Ⅰ)求A1B与平面ABD所成角的大小(结果用反三角函数值表示);
(Ⅱ)求点A1到平面AED的距离.
(19)(本小题满分12分)
已知c>0,设
P:函数y=cx在R上单调递减.
Q:不等式x+| x-2c | > 1 的解集为R.
如果P和Q有且仅有一个正确,求c的取值范围.
(20)(本小题满分12分)
在某海滨城市附近海面有一台风,据监测,当前台风中心位于城市O(如图)的东偏南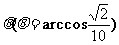 方向300 km的海面P处,并以20 km/h的速度向西偏北45°方向移动.台风侵袭的范围为圆形区域,当前半径为60 km,并以10 km/h的速度不断增大,问几小时后该城市开始受到台风的侵袭?
方向300 km的海面P处,并以20 km/h的速度向西偏北45°方向移动.台风侵袭的范围为圆形区域,当前半径为60 km,并以10 km/h的速度不断增大,问几小时后该城市开始受到台风的侵袭?

(21)(本小题满分14分)
已知常数a > 0,在矩形ABCD中,AB=4,BC=4a,O为AB的中点,点E、F、G分别在BC、CD、DA上移动,且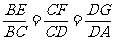 ,P为GE与OF的交点(如图).问是否存在两个定点,使P到这两点的距离的和为定值?若存在,求出这两点的坐标及此定值;若不存在,请说明理由.
,P为GE与OF的交点(如图).问是否存在两个定点,使P到这两点的距离的和为定值?若存在,求出这两点的坐标及此定值;若不存在,请说明理由.

(22)(本小题满分12分,附加题4分)
(Ⅰ)设{an}是集合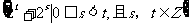 中所有的数从小到大排列成的数列,即a1=3,a2=5,a3=6,a4=9,a5=10,a6=12,……
中所有的数从小到大排列成的数列,即a1=3,a2=5,a3=6,a4=9,a5=10,a6=12,……
将数列{an}各项按照上小下大,左小右大的原则写成如下的三角形数表
(i)写出这个三角形数表的第四行、第五行各数;
(ii)求a100.
(Ⅱ)(本小题为附加题,如果解答正确,加4分,但全卷总分不超过150分)
设{bn}是集合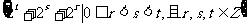 中所有的数从小到大排列成的数列,已知bk =1160,求k.
中所有的数从小到大排列成的数列,已知bk =1160,求k.
(13)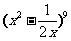 展开式中x9的系数是
.
展开式中x9的系数是
.
(14)使log2(-x)<x+1成立的x的取值范围是 .
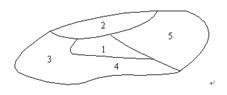
(15)如图,一个地区分为5个行政区域,现给地 图着色,要求相邻区域不得使用同一颜色,现有4种颜色可供选择,则不同的着色方法共有 种.(以数字作答)
(16)下列五个正方体图形中,l是正方体的一条对角线,点M、N、P分别为其所在棱的中点,能得出l⊥面MNP的图形的序号是 .(写出所有符合要求的图形序号)

(1)已知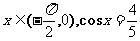 ,则tg 2x=
,则tg 2x=
(A)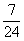 (B)
(B)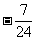 (C)
(C)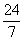 (D)
(D)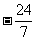
(2)圆锥曲线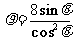 的准线方程是
的准线方程是
(A)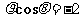 (B)
(B)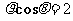 (C)
(C)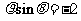 (D)
(D)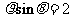
(3)设函数 若f(x0)>1,则x0的取值范围是
若f(x0)>1,则x0的取值范围是
(A)(-1,1) (B)(-1,+∞)
(C)(-∞,-2)∪(0,+∞) (D)(-∞,-1)∪(1,+∞)
(4)函数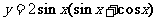 的最大值为
的最大值为
(A)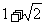 (B)
(B)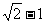 (C)
(C)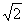 (D)2
(D)2
(5)已知圆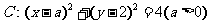 及直线
及直线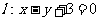 .当直线l被C截得的弦长为
.当直线l被C截得的弦长为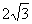 时,则a=
时,则a=
(A)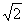 (B)
(B)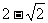 (C)
(C)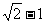 (D)
(D)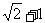
(6)已知圆锥的底面半径为R,高为3R,在它的所有内接圆柱中,全面积的最大值是
(A)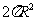 (B)
(B)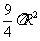 (C)
(C)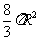 (D)
(D)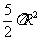
(7)已知方程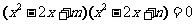 的四个根组成一个首项为
的四个根组成一个首项为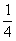 的等差数列,则
的等差数列,则
(A)1
(B)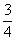 (C)
(C)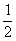 (D)
(D)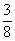
(8)已知双曲线中心在原点且一个焦点为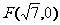 ,直线
,直线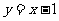 与其相交于M、N两点,MN中点的横坐标为
与其相交于M、N两点,MN中点的横坐标为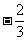 ,则此双曲线的方程是
,则此双曲线的方程是
(A)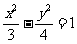 (B)
(B)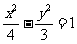 (C)
(C)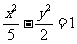 (D)
(D)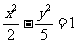
(9)函数f (x)=sinx,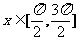 的反函数f-1(x)=
的反函数f-1(x)=
(A)-arcsinx,x∈[-1,1] (B)―π―arcsinx,x∈[-1,1]
(C)π+arcsinx,x∈[-1,1] (D)π-arcsinx,x∈[-1,1]
(10)已知长方形的四个顶点A(0,0),B(2,0),C(2,1)和D(0,1),一质点从AB的中点P0沿与AB夹角为θ的方向射到BC上的点P1后,依次反射到CD、DA和AB上的点P2、P3和P4(入射角等于反射角).设P4的坐标为(x4,0).若1< x4<2,则tgθ的取值范围是
(A)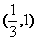 (B)
(B)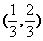 (C)
(C)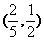 (D)
(D)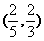
(11)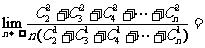
(A)3 (B)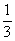 (C)
(C)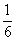 (D)6
(D)6
(12)一个四面体的所有棱长都为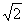 ,四个顶点在同一球面上,则此球的表面积为
,四个顶点在同一球面上,则此球的表面积为
(A)3π
(B)4π
(C)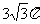 (D)6π
(D)6π
第Ⅱ卷
(17)(本小题满分12分)
已知α为第二象限角,且 sinα=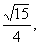 求
求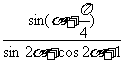 的值.
的值.
(18)(本小题满分12分)
已知数列{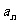 }为等比数列,
}为等比数列,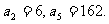
(Ⅰ)求数列{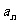 }的通项公式;
}的通项公式;
(Ⅱ)设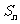 是数列{
是数列{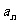 }的前
}的前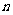 项和,证明
项和,证明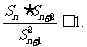
(19)(本小题满分12分)
已知直线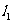 为曲线
为曲线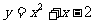 在点(1,0)处的切线,
在点(1,0)处的切线,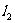 为该曲线的另一条切线,且
为该曲线的另一条切线,且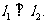
(Ⅰ)求直线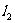 的方程;
的方程;
(Ⅱ)求由直线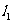 、
、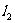 和
和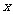 轴所围成的三角形的面积.
轴所围成的三角形的面积.
(20)(本小题满分12分)
某同学参加科普知识竞赛,需回答3个问题.竞赛规则规定:答对第一、二、三问题分别得100分、100分、200分,答错得零分.假设这名同学答对第一、二、三个问题的概率分别为0.8、0.7、0.6,且各题答对与否相互之间没有影响.
(Ⅰ)求这名同学得300分的概率;
(Ⅱ)求这名同学至少得300分的概率.
(21)(本小题满分12分)
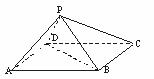
如图,四棱锥P-ABCD中,底面ABCD 为矩形,AB=8,AD=4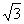 ,侧面PAD为等边三角形,并且与底面所成二面角为60°.
,侧面PAD为等边三角形,并且与底面所成二面角为60°.
(Ⅰ)求四棱锥P-ABCD的体积;
(Ⅱ)证明PA⊥BD.
(22)(本小题满分14分)
双曲线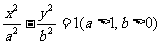 的焦距为2c,直线
的焦距为2c,直线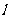 过点(a,0)和(0,b),且点(1,0)到直线
过点(a,0)和(0,b),且点(1,0)到直线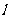 的距离与点(-1,0)到直线
的距离与点(-1,0)到直线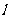 的距离之和
的距离之和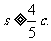 求双曲线的离心率e的取值范围.
求双曲线的离心率e的取值范围.
(13)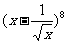 展开式中
展开式中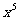 的系数为
.
的系数为
.
(14)已知函数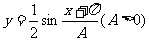 的最小正周期为3
的最小正周期为3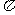 ,则A=
.
,则A=
.
(15)向量a、b满足(a-b)·(2a+b)=-4,且|a|=2,|b|=4,则a与b夹角的余弦值等于 .
(16)设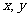 满足约束条件:
满足约束条件:

则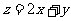 的最大值是
.
的最大值是
.
一项是符合题目要求的.
(1)设集合U={1,2,3,4,5},集合M={0,3,5},N={1,4,5},则M∩( U N)=
(A){5} (B){0,3} (C){0,2,3,5} (D) {0,1,3,4,5}
(2)函数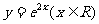 的反函数为
的反函数为
(A)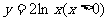 (B)
(B)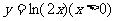
(C)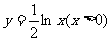 (D)
(D)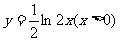
(3)正三棱柱侧面的一条对角线长为2,且与底面成45°角,则此三棱柱的体积为 (A)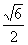 (B)
(B) 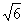 (C)
(C)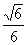 (D)
(D) 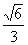
(4) 函数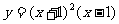 在
在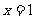 处的导数等于
处的导数等于
(A)1 (B)2 (C)3 (D)4
(5)为了得到函数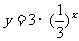 的图象,可以把函数
的图象,可以把函数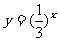 的图象
的图象
(A)向左平移3个单位长度 (B)向右平移3个单位长度
(C)向左平移1个单位长度 (D)向右平移1个单位长度
(6)等差数列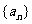 中,
中,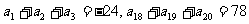 ,则此数列前20项和等于
,则此数列前20项和等于
(A)160 (B)180 (C)200 (D)220
(7)已知函数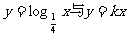 的图象有公共点A,且点A的横坐标为2,则
的图象有公共点A,且点A的横坐标为2,则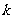
(A)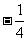 (B)
(B)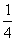 (C)
(C)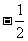 (D)
(D)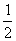
(8)已知圆C的半径为2,圆心在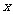 轴的正半轴上,直线
轴的正半轴上,直线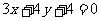 与圆C相切,则圆C的方程为
与圆C相切,则圆C的方程为
(A)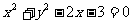 (B)
(B)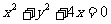
(C)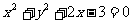 (D)
(D)
(9) 从5位男教师和4位女教师中选出3位教师,派到3个班担任班主任(每班1位班任),要求这3位班主任中男、女教师都要有,则不同的选派方案共有
(A)210种 (B)420种 (C)630种 (D)840种
(10)函数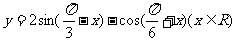 的最小值等于
的最小值等于
(A)-3 (B)-2 (C)-1 (D)-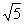
(11)已知球的表面积为20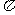 ,球面上有A、B、C三点.如果AB=AC=BC=2
,球面上有A、B、C三点.如果AB=AC=BC=2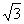 ,则球心到平面ABC的距离为
,则球心到平面ABC的距离为
(A)1 (B)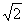 (C)
(C)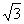 (D)2
(D)2
(12)△ABC中,a、b、c分别为∠A、∠B、∠C的对边.如果a、b、c成等差数列,
∠B=30°,△ABC的面积为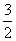 ,那么b=
,那么b=
(A)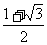 (B)
(B)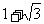 (C)
(C)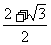 (D)
(D)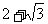
第Ⅱ卷
(17)(本小题满分12分)
解方程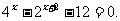
(18)(本小题满分12分)
已知α为锐角,且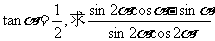 的值.
的值.
(19)(本上题满分12分)
设数列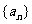 是公差不为零的等差数列,Sn是数列
是公差不为零的等差数列,Sn是数列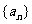 的前n项和,且
的前n项和,且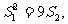
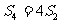 ,求数列
,求数列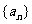 的通项公式.
的通项公式.
(20)(本小题满分12分)
某村计划建造一个室内面积为800m2的矩形蔬菜温室,在温室内,沿左、右两侧与后侧内墙各保留1m宽的通道,沿前侧内墙保留3m宽的空地。当矩形温室的边长各为多少时,蔬菜的种植面积最大?最大种植面积是多少?
(21)(本小题满分12分)
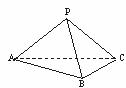
三棱锥P-ABC中,侧面PAC与底面ABC垂直,PA=PB=PC=3.
(1) 求证AB⊥BC;
(2) 如果AB=BC=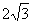 ,求侧面PBC与侧面PAC所成二面角的大小.
,求侧面PBC与侧面PAC所成二面角的大小.
(22)(本小题满分14分)
设椭圆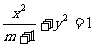 的两个焦点是
的两个焦点是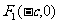 与
与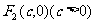 ,且椭圆上存在点P,使得直线PF2与直线PF2垂直.
,且椭圆上存在点P,使得直线PF2与直线PF2垂直.
(1)求实数m的取值范围;
(2)设L是相应于焦点F2的准线,直线PF2与L相交于点Q. 若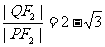 ,求直线PF2的方程.
,求直线PF2的方程.
(13)函数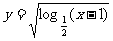 的定义域是
.
的定义域是
.
(14)用平面α截半径为R的球,如果球心到平面α的距离为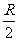 ,那么截得小圆的面积与球的表面积的比值为
.
,那么截得小圆的面积与球的表面积的比值为
.
(15)函数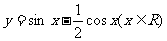 的最大值为
.
的最大值为
.
(16) 设P为圆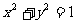 上的动点,则点P到直线
上的动点,则点P到直线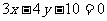 的距离的最小值为
的距离的最小值为
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com