
20.(本小题满分13分)如图,在长方体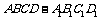 中,
中,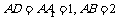 ,点E在棱
,点E在棱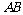 上移动。
上移动。
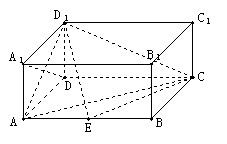 (1)证明:
(1)证明: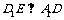 ;
;
(2)当E为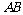 的中点时,求点E到面
的中点时,求点E到面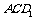 的距离;
的距离;
(3)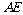 等于何值时,二面角
等于何值时,二面角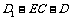 的大小为
的大小为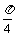 .
.
19.(本小题满分13分)定义在R上的单调函数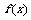 满足
满足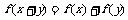 ,且
,且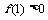 .
.
(1)判断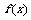 的奇偶性,并加以证明;
的奇偶性,并加以证明;
(2)当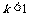 时,求满足不等式
时,求满足不等式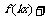
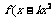
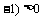 的
的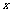 的取值范围.
的取值范围.
18.(本小题满分13分)用一枚质地均匀的硬币,甲、乙两人做抛掷硬币游戏,甲抛掷4次,记正面向上的次数为 ;乙抛掷3次,记正面向上的次数为
;乙抛掷3次,记正面向上的次数为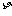 .
.
(1)分别求 和
和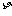 的期望;
的期望;
(2)规定:若 ,则甲获胜;否则,乙获胜.求甲获胜的概率.
,则甲获胜;否则,乙获胜.求甲获胜的概率.
17.(本小题满分13分)已知函数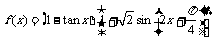 ,求
,求
(1)函数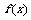 的定义域和值域;
的定义域和值域;
(2)写出函数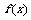 的单调递增区间.
的单调递增区间.
16.如果函数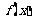 满足:对任意实数
满足:对任意实数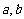 都有
都有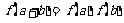 ,且
,且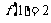 ,则
,则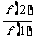
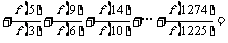 ______
______
15.已知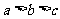 ,若不等式
,若不等式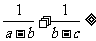
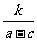 恒成立,则
恒成立,则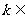 _________
_________
14.若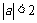 ,则
,则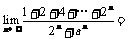 _______
_______
13.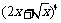 的展开式中
的展开式中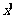 的系数是
的系数是
12.2005年10月12日,第五届亚太城市市长峰会在重庆会展中心隆重开幕。会议期间,为满足会议工作人员的需要,某宾馆将并排的4个房间安排给4个工作人员临时休息。假定每个人可以进入任一房间,且进入各个房间是等可能的,则每个房间恰好进去1人的概率是___________
11.已知函数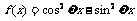 的最小正周期是
的最小正周期是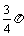 ,则实数
,则实数 =
=
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com