
(17)(本题满分12分)
已知复数z1=cos-i,z2=sin+i,求|z1·z2|的最大值和最小值.
(18)(本题满分12分)
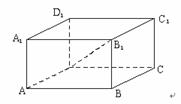
已知平行六面体ABCD-A1B1C1D1中,A1A⊥平面ABCD,AB=4,AD=2.若B1D⊥BC,直线B1D与平面ABCD所成的角等于30°,求平行六面体ABCD-A1B1C1D1的体积.
(19)(本题满分14分)本题共有2个小题,第1小满分5分,第2小题满分9分.
已知数列{an}(n为正整数)是首项为a1,公比为q的等比数列.
(1)求和: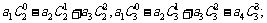
(2)由(1)的结果归纳概括出关于正整数n的一个结论,并加以证明;
(20)(本题满分14分)本题共有2个小题,第1小题满分6分,第2小题满分8分.
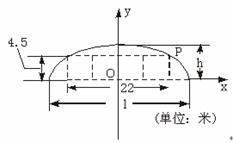
某隧道设计为以双向四车道,车道总宽22米,要求通行车辆限高4.5米,隧道全长2.5千米,隧道的拱线近似地看成半个随圆的形状.
(1)若最大拱高h为6米,则隧道设计的拱宽l是多少?
(2)若最大拱高h不小于6米,则应如何设计拱高h和拱宽l,才能使半个椭圆形隧道的土方工程量最小?(半个椭圆的面积公式为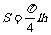 ,柱体体积为:底面积乘以高,本题结果均精确到0.1米)
,柱体体积为:底面积乘以高,本题结果均精确到0.1米)
(21)(本题满分16分)本题共有3个小题,第1小题满分4分,第2小题满分5分,第3小题满分7分.
在以O为原点的直角坐标系中,点A(4,-3)为△OAB的直角顶点,已知|AB|=2|OA|,且点B的纵坐标大于零.
(1)求向量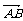 的坐标;
的坐标;
(2)求圆x2-6x+y2+2y=0关于直线OB对称的圆的方程;
(3)是否存在实数a,使抛物线y=ax2-1上总有关于直线OB对称的两个点?若不存在,说明理由;若存在,求a的取值范围.
(22)(本题满分18分)本题共有3个小题,第1小题满分5分,第2小题满分86分,第3小题满分7分.
已知集合M是满足下列性质的函数f(x)的全体;存在非零常数T,对任意x∈R,有f(x+T)=T f(x)成立.
(1)函数f(x)=x是否属于集合M?说明理由;
(2)设函数f(x)=ax(a >0且a≠1)的图象y=x与的图象有公共点,证明:f(x)= ax∈M;
(3)若函数f(x)=sink x∈M,求实数k的取值范围.
|
符号意义 |
本试卷所有符号 |
等同于《实验教材》符号 |
|
正切、余切 |
tg、ctg |
tan、cot |
(13)下列函数中,既为偶函数又在(0,)上单调递增的是
(A)y=tg|x|. (B)y=cos(-x).
(C)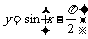 (D)
(D)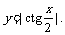
(14)在下列条件中,可判断平面α与β平行的是
(A)α、β都垂直于平面γ.
(B)α内存在不共线的三点到β的距离相等.
(C)l,m是α内两条直线,且l∥β,m∥β
(D)l,m是两条异面直线,且l∥α,m∥α,l∥β,m∥β
(15)设a1、b1、c1、a2、b2、c2均为非零实数,不等式a1x2+b1x+c1>0和 a2x2+b2x+c2>0的解集分别为集合M和N,那么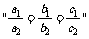 是“M=N”的
是“M=N”的
(A)充分非必要条件. (B)必要非充分条件 .
(C)充要条件. (D)既非充分又非必要条件.
(16)f(x)是定义在区间[-c,c]上的奇函数,其图像如图所示.令g(x)=af(x)+b,则下列关于函数g(x)的叙述正确的是
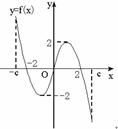
(A)若a<0,则函数g(x)的图像关于原点对称.
(B)若a=1,0<b<2,则方程g(x)=0有大于2的实根.
(C)若a=-2,b=0,则函数g(x)的图像关于y轴对称.
(D)若a≠1, b=2,则方程g(x)=0有三个实根.
(1)函数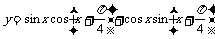 的最小正周期T=
.
的最小正周期T=
.
(2)若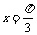 是方程2cos(x+)=1的解,其中∈(0,2),则=
.
是方程2cos(x+)=1的解,其中∈(0,2),则=
.
(3)在等差数列{an}中,a5=3,a6=-2,则a4+a5+…+a10= .
(4)在极坐标系中,定点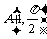 ,点B在直线cos+sin=0上运动,当线段AB最短时,点B的坐标是
.
,点B在直线cos+sin=0上运动,当线段AB最短时,点B的坐标是
.
(5)在正四棱锥P-ABCD中,若侧面与底面所成二面角的大小为60°,则异面直线PA与BC所成的大小等于 .(结果用反三角函数值表示)
(6)设集合A={x| |x|<4},B={x| x2-4x+3<4},则集合{x| x∈A且x A∩B }= .(7)在△ABC中,sinA:sinB:sinC=2:3:4,则∠ABC= .(结果用反三解函数值表示)
(8)若首项为a1,公比为q的等比数列{an}的前n项和总小于这个数列的各项和,则首项a1,公比q的一组取值可以是(a1,q)= .
(9)某国际科研合作项目成员由11个美国人、4个法国人和5个中国人组成。现从中随机选出两位作为成果发布人,则此两人不属于同一个国家的概率为 .(结果用分数表示)
(10)方程x3+lgx=18的根x≈ .(结果精确到0.1)
(11)已知点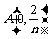 ,
,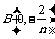 ,
,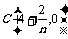 ,其中n为正整数.设Sn表示△ABC外接圆的面积,则
,其中n为正整数.设Sn表示△ABC外接圆的面积,则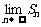 =
.
=
.
(12)给出问题:是F1、F2双曲线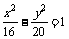 的焦点,点P在双曲线上.若点P到焦点F1的距离等于9,求点P到焦点的F2距离.某学生的解答如下:双曲线的实轴上为8,由||PF1|-|
PF2||=8,即|9-|
PF2||=8,得| PF2|=1或17.
的焦点,点P在双曲线上.若点P到焦点F1的距离等于9,求点P到焦点的F2距离.某学生的解答如下:双曲线的实轴上为8,由||PF1|-|
PF2||=8,即|9-|
PF2||=8,得| PF2|=1或17.
该学生的解答是否正确?若正确,请将他的解题依据填在下面空格内;或不正确,将正确结果填在下面空格内.
.
(15)(本小题满分13分)
已知函数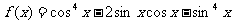
(Ⅰ)求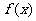 的最小正周期;
的最小正周期;
(Ⅱ)若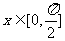 ,求
,求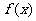 的最大值、最小值.
的最大值、最小值.
(16)(本小题满分13分)
已知数列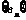 是等差数列,且
是等差数列,且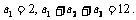
(Ⅰ)求数列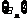 的通项公式;
的通项公式;
(Ⅱ)令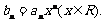 求数列
求数列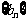 前n项和的公式.
前n项和的公式.
(17)(本小题满分15分)
如图,正三棱柱ABC-A1B1C1的底面边长的3,侧棱AA1=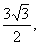 D是CB延长线上一点,且BD=BC.
D是CB延长线上一点,且BD=BC.
(Ⅰ)求证:直线BC1//平面AB1D;
(Ⅱ)求二面角B1-AD-B的大小;
(Ⅲ)求三棱锥C1-ABB1的体积.

(18)(本小题满分15分)
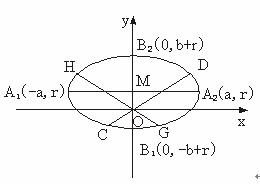
如图,椭圆的长轴A1A2与x轴平行,短轴B1B2在y轴上,中心为M(0,r)(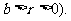
(Ⅰ)写出椭圆的方程,求椭圆的焦点坐标及离心率;
(Ⅱ)直线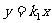 交椭圆于两点
交椭圆于两点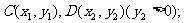 直线
直线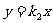 交椭圆于两点
交椭圆于两点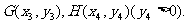 求证:
求证: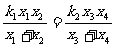 ;
;
(Ⅲ)对于(Ⅱ)中的C,D,G,H,设CH交x轴于点P,GD交x轴于点Q.
求证:|OP|=|OQ|. (证明过程不考虑CH或GD垂直于x轴的情形)
(19)(本小题满分14分)
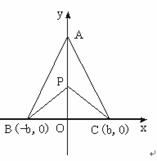
有三个新兴城镇,分别位于A,B,C三点处,且AB=AC=a,BC=2b.今计划合建一个中心医院,为同时方便三镇,准备建在BC的垂直平分线上的P点处,(建立坐标系如图)
(Ⅰ)若希望点P到三镇距离的平方和为最小, 点P应位于何处?
(Ⅱ)若希望点P到三镇的最远距离为最小, 点P应位于何处?
(20)(本小题满分14分)
设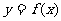 是定义在区间
是定义在区间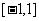 上的函数,且满足条件:
上的函数,且满足条件:
(i)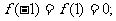
(ii)对任意的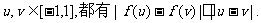
(Ⅰ)证明:对任意的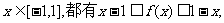
(Ⅱ)证明:对任意的
(Ⅲ)在区间[-1,1]上是否存在满足题设条件的奇函数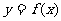 ,且使得
,且使得

若存在,请举一例:若不存在,请说明理由.
(11)函数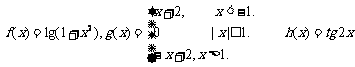 中,
是偶函数.
中,
是偶函数.
(12)以双曲线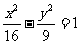 右顶点为顶点,左焦点为焦点的抛物线的方程是
右顶点为顶点,左焦点为焦点的抛物线的方程是
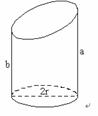
(13)如图,已知底面半径为r的圆柱被一个平面所截,剩下部分母线长的最大值为a,最小值为b,那么圆柱被截后剩下部分的体积是 .
(14)将长度为1的铁丝分成两段,分别围成一个正方形和一个圆形,要使正方形与圆的面积之和最小,正方形的周长应为 .
(1)设集合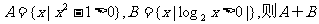 等于
等于
(A)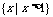 (B)
(B)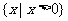 (C)
(C)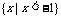 (D)
(D)
(2)设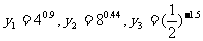 ,则
,则
(A)y3>y1>y2 (B)y2>y1>y3 (C)y1>y2>y3 (D)y1>y3>y2
(3)“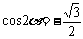 ”是“
”是“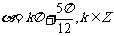 ”的
”的
(A)必要非充分条件 (B)充分非必要条件
(C)充分必要条件 (D)既非充分又非必要条件
(4)已知α,β是平面,m,n是直线.下列命题中不正确的是
(A)若m∥n,m⊥α,则n⊥α (B)若m∥α,α∩β=n,则m∥n
(C)若m⊥α,m⊥β,则α∥β (D)若m⊥α,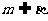 ,则α⊥β
,则α⊥β
(5)极坐标方程 表示的曲线是
表示的曲线是
(A)圆 (B)椭圆 (C)抛物线 (D)双曲线
(6)若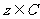 且
且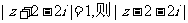 的最小值是
的最小值是
(A)2 (B)3 (C)4 (D)5
(7)如果圆台的母线与底面成60°角,那么这个圆台的侧面积与轴截面面积的比为
(A)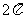 (B)
(B)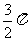 (C)
(C)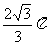 (D)
(D)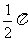
(8)从黄瓜、白菜、油菜、扁豆4种蔬菜品种中选出3种,分别种在不同土质的三块土地上,其中黄瓜必须种植,不同的种植方法共有
(A)24种 (B)18种 (C)12种 (D)6种
(9)若数列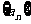 的通项公式是
的通项公式是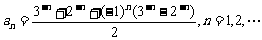 ,则
,则 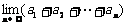 等于
等于
(A)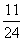 (B)
(B)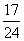 (C)
(C)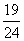 (D)
(D)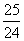
(10)某班试用电子投票系统选举班干部候选人.全班k名同学都有选举权和被选举权,他们的编号分别为1,2,…,k,规定:同意按“1”,不同意(含弃权)按“0”,令
 , 其中i=1,2,…,k,且j=1,2,…,k,则同时同意第1,2号同学当选的人数为
, 其中i=1,2,…,k,且j=1,2,…,k,则同时同意第1,2号同学当选的人数为
(A)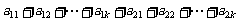
(B)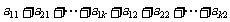
(C)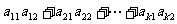 (D)
(D)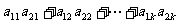
第Ⅱ卷
(17)(本小题满分12分)
有三种产品,合格率分别是0.90,0.95和0.95,各抽取一件进行检验.
(Ⅰ)求恰有一件不合格的概率;(Ⅱ)求至少有两件不合格的概率.(精确到0.001)
(18)(本小题满分12分)
已知函数 上R上的偶函数,其图象关于点
上R上的偶函数,其图象关于点 对称,且在区间
对称,且在区间 上是单调函数,求
上是单调函数,求 和ω的值.
和ω的值.
(19)(本小题满分12分)
如图,直三棱柱ABC-A1B1C1中,底面是等腰直角三角形,∠ACB=90°,侧棱AA1=2,D、E分别是CC1与A1B的中点,点E在平面ABD上的射影是△ABD的重心G.
(Ⅰ)求A1B与平面ABD所成角的大小(结果用反三角函数值表示);
(Ⅱ)求点A1到平面AED的距离.

(20)(本小题满分12分)
已知常数 ,向量
,向量 经过原点O以
经过原点O以 为方向向量的直线与经过定点A(0,a)以
为方向向量的直线与经过定点A(0,a)以 为方向向量的直线相交于点P,其中
为方向向量的直线相交于点P,其中 试问:是否存在两个定点E、F,使得|PE|+|PF|为定值.若存在,求出E、F的坐标;若不存在,说明理由.
试问:是否存在两个定点E、F,使得|PE|+|PF|为定值.若存在,求出E、F的坐标;若不存在,说明理由.
(21)(本小题满分12分)
已知 为正整数.
为正整数.
(Ⅰ)设 ;
;
(Ⅱ)设
(22)(本小题满分14分)
设 如图,已知直线
如图,已知直线 及曲线C:
及曲线C: ,C上的点Q1的横坐标为
,C上的点Q1的横坐标为 (
( ).从C上的点Qn(n≥1)作直线平行于x轴,交直线l于点
).从C上的点Qn(n≥1)作直线平行于x轴,交直线l于点 ,再从点
,再从点 作直线平行于y轴,交曲线C于点Qn+1.Qn(n=1,2,3,…)的横坐标构成数列
作直线平行于y轴,交曲线C于点Qn+1.Qn(n=1,2,3,…)的横坐标构成数列
(Ⅰ)试求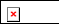 的关系,并求
的关系,并求 的通项公式;
的通项公式;
(Ⅱ)当 时,证明
时,证明 ;
;
(Ⅲ)当a=1时,证明
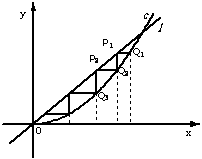
(13) 展开式中x9的系数是
.
展开式中x9的系数是
.
(14)某公司生产三种型号的轿车,产量分别为1200辆,6000辆和2000辆,为检验该公司的产品质量,现用分层抽样的方法抽取46辆进行检验,这三种型号的轿车依次应抽取 , , 辆.
(15)某城市在中心广场建造一个花圃,花圃分为6个部分(如图).现要栽种4种不同颜色的花,每部分栽种一种且相邻部分不能栽种同样颜色的花,不同的栽种方法有 种.(以数字作答)

(16)对于四面体ABCD,给出下列四个命题
①若AB=AC,BD=CD,则BC⊥AD. ②若AB=CD,AC=BD,则BC⊥AD.
③若AB⊥AC,BD⊥CD,则BC⊥AD. ④若AB⊥CD,BD⊥AC,则BC⊥AD.
其中真命题的序号是 .(写出所有真命题的序号)
(1)如果函数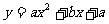 的图像与x轴有两上交点,则点(a,b)在aOb平面上的区域(不包含边界)为
的图像与x轴有两上交点,则点(a,b)在aOb平面上的区域(不包含边界)为

(2)抛物线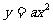 的准线方程是y=2,则a的值为
的准线方程是y=2,则a的值为
(A)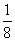 (B)-
(B)-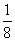 (C)8 (D)-8
(C)8 (D)-8
(3)已知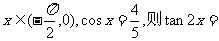
(A)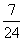 (B)-
(B)-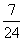 (C)
(C)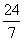 (D)-
(D)-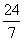
(4)设函数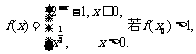 则x0的取值范围是
则x0的取值范围是
(A)(-1,1) (B)(-1,+∞)
(C)(-∞,-2)∪(0,+∞) (D)(-∞,-1)∪(1,+∞)
(5)O是平面上一定点,A、B、C是平面上不共线的三个点,动点P满足
 则P的轨迹一定通过△ABC的( )
则P的轨迹一定通过△ABC的( )
(A)外心 (B)内心 (C)重心 (D)垂心
(6)函数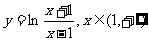 的反函数为
的反函数为
(A)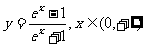 (B)
(B)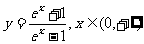
(C)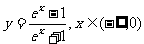 (D)
(D)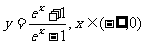
(7)棱长为a的正方体中,连结相邻面的中心,以这些线段为棱的八面体的体积为
(A)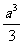 (B)
(B)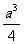 (C)
(C)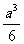 (D)
(D)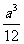
(8)设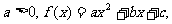 曲线
曲线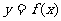 在点
在点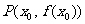 处切线的倾斜角的取值范围为
处切线的倾斜角的取值范围为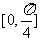 ,则P到曲线
,则P到曲线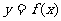 对称轴距离的取值范围为
对称轴距离的取值范围为
(A)[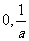 ] (B)
] (B)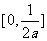 (C)
(C)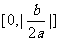 (D)
(D)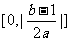
(9)已知方程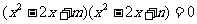 的四个根组成一个首项为
的四个根组成一个首项为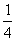 的等差数列,则 |m-n|=
的等差数列,则 |m-n|=
(A)1 (B)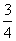 (C)
(C)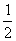 (D)
(D)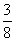
(10)已知双曲线中心在原点且一个焦点为F(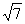 ,0)直线y=x-1与其相交于M、N两点,MN中点的横坐标为
,0)直线y=x-1与其相交于M、N两点,MN中点的横坐标为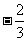 ,则此双曲线的方程是
,则此双曲线的方程是
(A)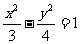 (B)
(B)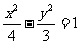 (C)
(C)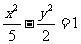 (D)
(D)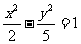
(11)已知长方形四个顶点A(0,0),B(2,0),C(2,1)和D(0,1).一质点从AB的中点P0沿与AB夹角为θ的方向射到BC上的点P1后,依次反射到CD、DA和AB上的点P2、P3和P4(入射角等于反射角).设P4的坐标为(x4,0).若1< x4<2,则tanθ的取值范围是
(A)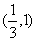 (B)
(B)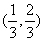 (C)
(C)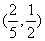 (D)
(D)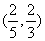
(12)一个四面体的所有棱长都为 ,四个顶点在同一球面上,则此球的表面积为
,四个顶点在同一球面上,则此球的表面积为
(A)3π (B)4π (C)  π (D)6π
π (D)6π
第Ⅱ卷
(17)(本小题满分12分)
已知正四棱柱ABCD-A1B1C1D1,AB=1,A A1=2,点E为CC1中点,点F为BD1中点.
(Ⅰ)证明EF为BD1与CC1的公垂线;
(Ⅱ)求点D1到面BDE的距离.
(18)(本小题满分12分)
已知复数z的辐角为60°,且| z-1 |是| z |和| z-2 |的等比中项,求| z |.
(19)(本小题满分12分)
已知a>0,a≠1,设
P:函数y=loga(x+1)在x∈(0,+∞)内单调递减.
Q:曲线y=x2+(2a-3)x+1 与轴交于不同两点.
如果P和Q有且仅有一个正确,求a的取值范围.
(20)(本小题满分12分)
在某海滨城市附近海面有一台风,据监测,当前台风中心位于城市O(如图)的东偏南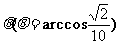 方向300 km的海面P处,并以20 km/h的速度向西偏北45°方向移动.台风侵袭的范围为圆形区域,当前半径为60 km,并以10 km/h的速度不断增大,问几小时后该城市开始受到台风的侵袭?
方向300 km的海面P处,并以20 km/h的速度向西偏北45°方向移动.台风侵袭的范围为圆形区域,当前半径为60 km,并以10 km/h的速度不断增大,问几小时后该城市开始受到台风的侵袭?

(21)(本小题满分14分)

已知常数a > 0,在矩形ABCD中,AB=4,BC=4a,O为AB的中点,点E、F、G分别在BC、CD、DA上移动,且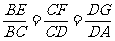 ,P为GE与OF的交点(如图).问是否存在两个定点,使P到这两点的距离的和为定值?若存在,求出这两点的坐标及此定值;若不存在,请说明理由.
,P为GE与OF的交点(如图).问是否存在两个定点,使P到这两点的距离的和为定值?若存在,求出这两点的坐标及此定值;若不存在,请说明理由.
(22)(新课程)(本小题满分14分)
设a0为常数,且an=3n-1-2an-1(n∈N+).
(Ⅰ)证明对任意n≥1, ;
;
(Ⅱ)假设对任意n≥1有an>an-1,求a0的取值范围.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com