
(1)已知向量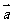 =(4,2),向量
=(4,2),向量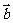 =(
=(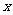 ,3),且
,3),且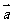 //
//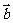 ,则
,则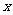 =( )
=( )
(A)9 (B)6 (C)5 (D)3
(2)已知集合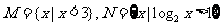 ,则
,则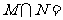 ( )
( )
(A)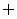 (B)
(B)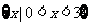 (C)
(C)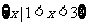 (D)
(D)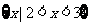
(3)函数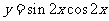 的最小正周期是( )
的最小正周期是( )
(A)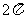 (B)
(B)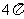 (C)
(C)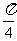 (D)
(D)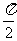
(4)如果函数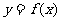 的图像与函数
的图像与函数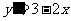 的图像关于坐标原点对称,则
的图像关于坐标原点对称,则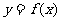 的表达式为( )
的表达式为( )
(A)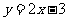 (B)
(B)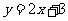 (C)
(C)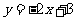 (D)
(D)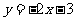
(5)已知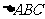 的顶点B、C在椭圆
的顶点B、C在椭圆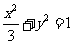 上,顶点A是椭圆的一个焦点,且椭圆的另外一个焦点在BC边上,则
上,顶点A是椭圆的一个焦点,且椭圆的另外一个焦点在BC边上,则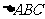 的周长是( )
的周长是( )
(A)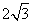 (B)6 (C)
(B)6 (C)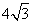 (D)12
(D)12
(6)已知等差数列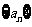 中,
中,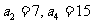 ,则前10项的和
,则前10项的和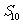 =( )
=( )
(A)100 (B)210 (C)380 (D)400
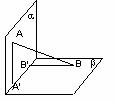
(7)如图,平面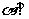 平面
平面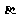 ,
,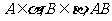 与两平面
与两平面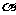 、
、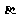 所成的角分别为
所成的角分别为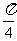 和
和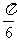 。过A、B分别作两平面交线的垂线,垂足为
。过A、B分别作两平面交线的垂线,垂足为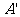 、
、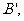 若AB=12,则
若AB=12,则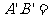 ( )
( )
 (A)4 (B)6 (C)8 (D)9
(A)4 (B)6 (C)8 (D)9
(8)已知函数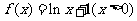 ,则
,则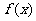 的反函数为( )
的反函数为( )
(A)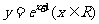 (B)
(B)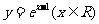
(C)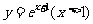 (D)
(D)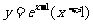
(9)已知双曲线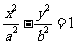 的一条渐近线方程为
的一条渐近线方程为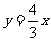 ,则双曲线的离心率为( )
,则双曲线的离心率为( )
(A)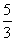 (B)
(B)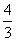 (C)
(C)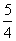 (D)
(D)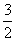
(10)若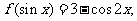 则
则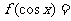 ( )
( )
(A)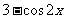 (B)
(B)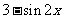 (C)
(C)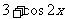 (D)
(D)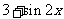
(11)过点(-1,0)作抛物线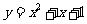 的切线,则其中一条切线为( )
的切线,则其中一条切线为( )
(A)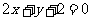 (B)
(B)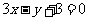 (C)
(C)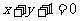 (D)
(D)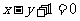
(12)5名志愿者分到3所学校支教,每个学校至少去一名志愿者,则不同的分派方法共有( )
(A)150种 (B)180种 (C)200种 (D)280种
第Ⅱ卷
(17)(本小题满分12分)
已知向量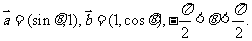
(Ⅰ)若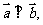 ,求θ;
,求θ;
(Ⅱ)求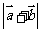 的最大值.
的最大值.
(18)(本小题满分12分)
某批产品成箱包装,每箱5件.一用户在购进该批产品前先取出3箱,再从每箱中任意抽取2件产品进行检验.设取出的第一、二、三箱中分别有0件、1件、2件二等品,其余为一等品.
(Ⅰ)用ξ表示抽检的6件产品中二等品的件数,求ξ的分布列及ξ的数学期望;
(Ⅱ)若抽检的6件产品中有2件或2件以上二等品,用户就拒绝购买这批产品,求这批产品级用户拒绝的概率.
(19)(本小题满分12分)
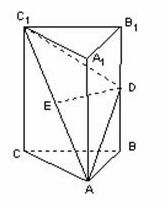
如图,在直三棱柱ABC-A1B1C1中,AB=BC,D、E分别为BB1、AC1的中点.
(Ⅰ)证明:ED为异面直线BB1与AC1的公垂线;
(Ⅱ)设AA1=AC=AB,求二面角A1-AD-C1的大小.
(20)(本小题满分12分)
设函数f(x)=(x+1)ln(x+1),若对所有的x≥0,都有f(x)≥ax成立,求实数a的取值范围.
(21)(本小题满分14分)
已知抛物线x2=4y的焦点为F,A、B是抛物线上的两动点,且=λ(λ>0).过A、B两点分别作抛物线的切线,设其交点为M.
(Ⅰ)证明·为定值;
(Ⅱ)设△ABM的面积为S,写出S=f(λ)的表达式,并求S的最小值.
(22)(本小题满分12分)
设数列{an}的前n项和为Sn,且方程x2-anx-an=0有一根为Sn-1,n=1,2,3,….
(Ⅰ)求a1,a2;
(Ⅱ){an}的通项公式.
(13)在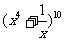 的展开式中常数项是
(用数字作答)
的展开式中常数项是
(用数字作答)
(14)已知△ABC的三个内角A、B、C成等差数列,且AB=1,BC=4,则边BC上的中线AD的长为 .
(15)过点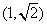 的直线l将圆(x-2)2+y2=4分成两段弧,当劣弧所对的圆心角最小时,直线l的斜率k=
.
的直线l将圆(x-2)2+y2=4分成两段弧,当劣弧所对的圆心角最小时,直线l的斜率k=
.
(16)一个社会调查机构就某地居民的月收入调查了10 000人,并根据所得数据画了样本的频率分布直方图(如下图).为了分析居民的收入与年龄、学历、职业等方面的关系,要从这10 000人中再用分层抽样方法抽出100人作进一步调查,则在[2500,3000)(元)月收入段应抽出

(1)已知集合M={x|x<3},N={x|log2x>1},则M∩N=
(A)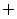 (B){x|0<x<3}
(B){x|0<x<3}
(C){x|1<x<3} (D){x|2<x<3}
(2)函数y=sin2xcos2x的最小正周期是

(3)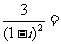

(4)过球的一条半径的中点,作垂直于该半径的平面,则所得截面的面积与球的表面积的比为

(5)已知△ABC的顶点B、C在椭圆+y2=1上,顶点A是椭圆的一个焦点,且椭圆的另外一个焦点在BC边上,则△ABC的周长是

(6)函数y=lnx-1(x>0)的反函数为
(A)y=ex+1(x∈R) (B)y=ex-1(x∈R)
(C)y=ex+1(x>1) (D) y=ex-1(x>1)
(7)如图,平面α⊥平面β,A∈α,B∈β,AB与两平面α、β所成的角分别为和,过A、B分别作两平面交线的垂线,垂足为A′、B′,则AB∶A′B′=

(A)2∶1 (B)3∶1 (C)3∶2 (D)4∶3
(8)函数y=f(x)的图像与函数g(x)=log2x(x>0)的图像关于原点对称,则f(x)的表达式为
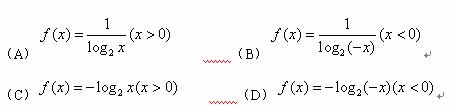
(9)已知双曲线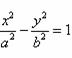 的一条渐近线方称为
的一条渐近线方称为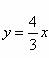 ,则双曲线的离心率为
,则双曲线的离心率为

(10)若f(sinx)=3-cos2x,则f(cosx)=
(A)3-cos2x (B)3-sin2x (C)3+cos2x (D)3+sin2x
(11)设Sn是等差数列{an}的前n项和,若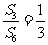 ,则
,则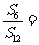

(12)函数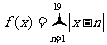 的最小值为
的最小值为
(A)190 (B)171 (C)90 (D)45
第Ⅱ卷
⒄、(本小题满分12分)
已知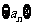 为等比数列,
为等比数列,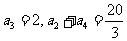 ,求
,求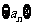 的通项式。
的通项式。
⒅、(本小题满分12分)
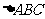 的三个内角为
的三个内角为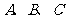 ,求当A为何值时,
,求当A为何值时, 取得最大值,并求出这个最大值。
取得最大值,并求出这个最大值。
⒆、(本小题满分12分)
A、B是治疗同一种疾病的两种药,用若干试验组进行对比试验。每个试验组由4只小白鼠组成,其中2只服用A,另2只服用B,然后观察疗效。若在一个试验组中,服用A有效的小白鼠的只数比服用B有效的多,就称该试验组为甲类组。设每只小白鼠服用A有效的概率为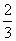 ,服用B有效的概率为
,服用B有效的概率为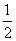 。
。
(Ⅰ)求一个试验组为甲类组的概率;
(Ⅱ)观察3个试验组,求这3个试验组中至少有一个甲类组的概率。
⒇、(本小题满分12分)
如图,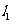 、
、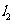 是互相垂直的异面直线,MN是它们的公垂线段。点A、B在
是互相垂直的异面直线,MN是它们的公垂线段。点A、B在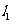 上,C在
上,C在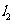 上,
上,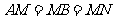 。
。
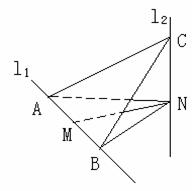
(Ⅰ)证明 ⊥
⊥ ;
;
(Ⅱ)若 ,求
,求 与平面ABC所成角的余弦值。
与平面ABC所成角的余弦值。
(21)、(本小题满分12分)
设P是椭圆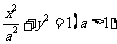 短轴的一个端点,
短轴的一个端点,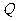 为椭圆上的一个动点,求
为椭圆上的一个动点,求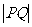 的最大值。
的最大值。
(22)、(本小题满分14分)
设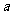 为实数,函数
为实数,函数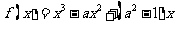 在
在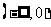 和
和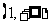 都是增函数,求
都是增函数,求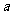 的取值范围。
的取值范围。
⒀、已知函数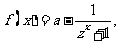 ,若
,若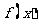 为奇函数,则
为奇函数,则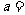 ________。
________。
⒁、已知正四棱锥的体积为12,底面对角线的长为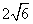 ,则侧面与底面所成的二面角等于_______________。
,则侧面与底面所成的二面角等于_______________。
⒂、设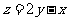 ,式中变量
,式中变量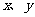 满足下列条件
满足下列条件
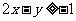
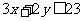
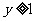
则z的最大值为_____________。
⒃、安排7位工作人员在5月1日到5月7日值班,每人值班一天,其中甲、乙二人都不能安排在5月1日和2日,不同的安排方法共有__________种。(用数字作答)
⑴、已知向量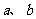 满足
满足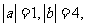 ,且
,且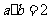 ,则
,则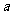 与
与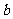 的夹角为
的夹角为
A.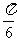 B.
B.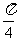 C.
C.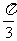 D.
D.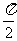
⑵、设集合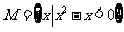 ,
,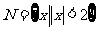 ,则
,则
A.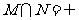 B.
B.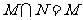
C.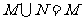 D.
D.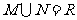
⑶、已知函数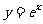 的图像与函数
的图像与函数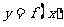 的图像关于直线
的图像关于直线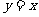 对称,则
对称,则
A.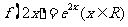 B.
B.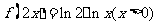
C.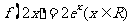 D.
D.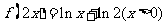
⑷、双曲线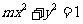 的虚轴长是实轴长的2倍,则
的虚轴长是实轴长的2倍,则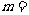
A.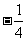 B.
B. C.
C.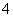 D.
D.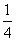
⑸、设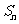 是等差数列
是等差数列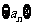 的前
的前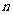 项和,若
项和,若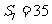 ,则
,则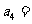
A.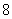 B.
B.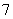 C.
C.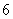 D.
D.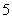
⑹、函数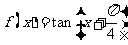 的单调增区间为
的单调增区间为
A.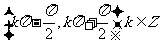 B.
B.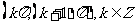
C.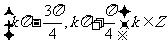 D.
D.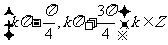
⑺、从圆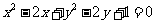 外一点
外一点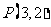 向这个圆作两条切线,则两切线夹角的余弦值为
向这个圆作两条切线,则两切线夹角的余弦值为
A.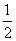 B.
B.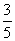 C.
C.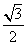 D.
D.
⑻、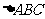 的内角A、B、C的对边分别为a、b、c,若a、b、c成等比数列,且
的内角A、B、C的对边分别为a、b、c,若a、b、c成等比数列,且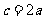 ,则
,则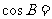
A.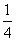 B.
B.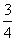 C.
C.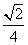 D.
D.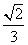
⑼、已知各顶点都在一个球面上的正四棱柱高为4,体积为16,则这个球的表面积是
A.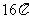 B.
B.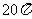 C.
C.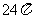 D.
D.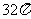
⑽、在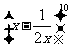 的展开式中,
的展开式中,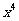 的系数为
的系数为
A.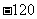 B.
B.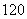 C.
C.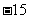 D.
D.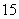
⑾、抛物线 上的点到直线
上的点到直线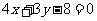 距离的最小值是
距离的最小值是
A.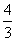 B.
B.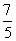 C.
C.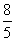 D.
D.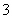
⑿、用长度分别为2、3、4、5、6(单位: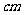 )的5根细木棒围成一个三角形(允许连接,但不允许折断),能够得到的三角形的最大面积为
)的5根细木棒围成一个三角形(允许连接,但不允许折断),能够得到的三角形的最大面积为
A.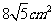 B.
B.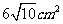 C.
C.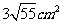 D.
D.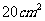
第Ⅱ卷
⒄、(本小题满分12分)
 的三个内角为
的三个内角为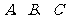 ,求当A为何值时,
,求当A为何值时, 取得最大值,并求出这个最大值。
取得最大值,并求出这个最大值。
⒅、(本小题满分12分)
A、B是治疗同一种疾病的两种药,用若干试验组进行对比试验。每个试验组由4只小白鼠组成,其中2只服用A,另2只服用B,然后观察疗效。若在一个试验组中,服用A有效的小白鼠的只数比服用B有效的多,就称该试验组为甲类组。设每只小白鼠服用A有效的概率为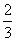 ,服用B有效的概率为
,服用B有效的概率为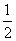 。
。
(Ⅰ)求一个试验组为甲类组的概率;
(Ⅱ)观察3个试验组,用 表示这3个试验组中甲类组的个数,求
表示这3个试验组中甲类组的个数,求 的分布列和数学期望。
的分布列和数学期望。
⒆、(本小题满分12分)
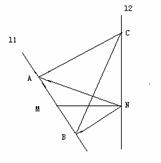 如图,
如图, 、
、 是互相垂直的异面直线,MN是它们的公垂线段。点A、B在
是互相垂直的异面直线,MN是它们的公垂线段。点A、B在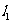 上,C在
上,C在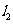 上,
上,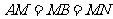 。
。
(Ⅰ)证明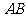 ⊥
⊥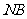 ;
;
(Ⅱ)若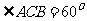 ,求
,求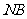 与平面ABC所成角的余弦值。
与平面ABC所成角的余弦值。
⒇、(本小题满分12分)
在平面直角坐标系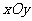 中,有一个以
中,有一个以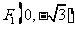 和
和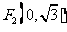 为焦点、离心率为
为焦点、离心率为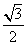 的椭圆,设椭圆在第一象限的部分为曲线C,动点P在C上,C在点P处的切线与
的椭圆,设椭圆在第一象限的部分为曲线C,动点P在C上,C在点P处的切线与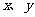 轴的交点分别为A、B,且向量
轴的交点分别为A、B,且向量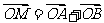 。求:
。求:
(Ⅰ)点M的轨迹方程;
(Ⅱ)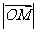 的最小值。
的最小值。
(21)、(本小题满分14分)
已知函数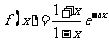 。
。
(Ⅰ)设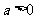 ,讨论
,讨论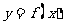 的单调性;
的单调性;
(Ⅱ)若对任意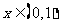 恒有
恒有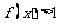 ,求
,求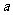 的取值范围。
的取值范围。
(22)、(本小题满分12分)
设数列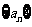 的前
的前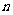 项的和
项的和
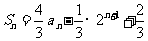 ,
,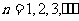
(Ⅰ)求首项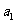 与通项
与通项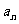 ;
;
(Ⅱ)设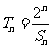 ,
,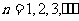 ,证明:
,证明: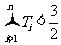
⒀、已知正四棱锥的体积为12,底面对角线的长为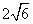 ,则侧面与底面所成的二面角等于_______________。
,则侧面与底面所成的二面角等于_______________。
⒁、设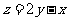 ,式中变量
,式中变量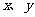 满足下列条件
满足下列条件
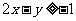
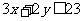
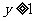
则z的最大值为_____________。
⒂、安排7位工作人员在5月1日到5月7日值班,每人值班一天,其中甲、乙二人都不能安排在5月1日和2日,不同的安排方法共有__________种。(用数字作答)
⒃、设函数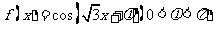 。若
。若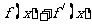 是奇函数,则
是奇函数,则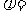 __________。
__________。
⑴、设集合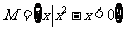 ,
,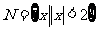 ,则
,则
A.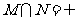 B.
B.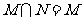
C.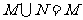 D.
D.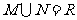
⑵、已知函数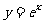 的图像与函数
的图像与函数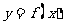 的图像关于直线
的图像关于直线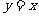 对称,则
对称,则
A.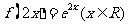 B.
B.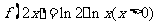
C.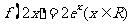 D.
D.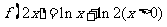
⑶、双曲线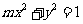 的虚轴长是实轴长的2倍,则
的虚轴长是实轴长的2倍,则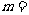
A.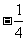 B.
B. C.
C.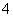 D.
D.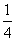
⑷、如果复数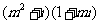 是实数,则实数
是实数,则实数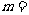
A.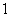 B.
B. C.
C.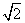 D.
D.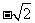
⑸、函数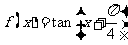 的单调增区间为
的单调增区间为
A.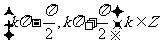 B.
B.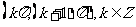
C.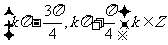 D.
D.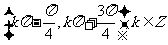
⑹、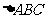 的内角A、B、C的对边分别为a、b、c,若a、b、c成等比数列,且
的内角A、B、C的对边分别为a、b、c,若a、b、c成等比数列,且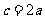 ,则
,则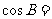
A.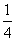 B.
B.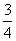 C.
C.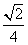 D.
D.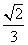
⑺、已知各顶点都在一个球面上的正四棱柱高为4,体积为16,则这个球的表面积是
A.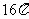 B.
B.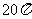 C.
C.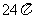 D.
D.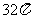
⑻、抛物线 上的点到直线
上的点到直线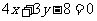 距离的最小值是
距离的最小值是
A.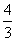 B.
B.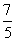 C.
C.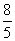 D.
D.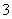
⑼、设平面向量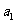 、
、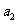 、
、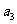 的和
的和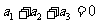 。如果向量
。如果向量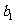 、
、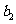 、
、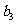 ,满足
,满足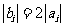 ,且
,且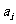 顺时针旋转
顺时针旋转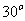 后与
后与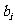 同向,其中
同向,其中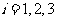 ,则
,则
A.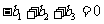 B.
B.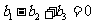
C.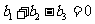 D.
D.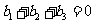
⑽、设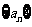 是公差为正数的等差数列,若
是公差为正数的等差数列,若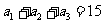 ,
,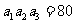 ,则
,则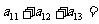
A.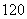 B.
B.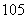 C.
C.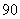 D.
D.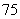
⑾、用长度分别为2、3、4、5、6(单位: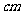 )的5根细木棒围成一个三角形(允许连接,但不允许折断),能够得到的三角形的最大面积为
)的5根细木棒围成一个三角形(允许连接,但不允许折断),能够得到的三角形的最大面积为
A.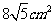 B.
B.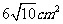 C.
C.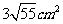 D.
D.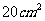
⑿、设集合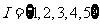 。选择I的两个非空子集A和B,要使B中最小的数大于A中最大的数,则不同的选择方法共有
。选择I的两个非空子集A和B,要使B中最小的数大于A中最大的数,则不同的选择方法共有
A.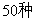 B.
B.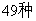 C.
C.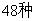 D.
D.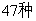
第Ⅱ卷
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com