
1.已知α为第三象限角,则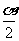 所在的象限是 ( )
所在的象限是 ( )
A.第一或第二象限 B.第二或第三象限
C.第一或第三象限 D.第二或第四象限
(17)(本小题满分12分)
已知向量m=(cosθ,sinθ)和n=(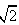 -sinθ,cosθ),θ∈(π,2π),且|m+n|=
-sinθ,cosθ),θ∈(π,2π),且|m+n|= 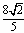
,求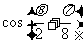 的值.
的值.
(18)(本小题满分12分)
袋中装有黑球和白球共7个,从中任取2个球都是白球的概率为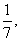 现有甲、乙两人从袋中轮流摸取1球,甲先取,乙后取,然后甲再取……取后不放回,直到两人中有一人取到白球时既终止,每个球在每一次被取出的机会是等可能的。
现有甲、乙两人从袋中轮流摸取1球,甲先取,乙后取,然后甲再取……取后不放回,直到两人中有一人取到白球时既终止,每个球在每一次被取出的机会是等可能的。
(I)求袋中原有的白球的个数;
(II)求取球2次终止的概率;
(III)求甲取到白球的概率.
(19)(本小题满分12分)
已知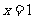 是函数
是函数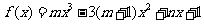 的一个极值点,其中
的一个极值点,其中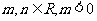 ,
,
(I)求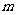 与
与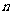 的关系式;(II)求
的关系式;(II)求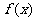 的单调区间;
的单调区间;
(20)(本小题满分12分)
如图,已知长方体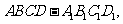
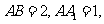 直线
直线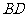 与平面
与平面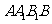 所成的角为
所成的角为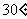 ,
,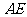 垂直
垂直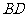 于
于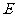 ,
,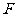 为
为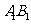 的中点.
的中点.
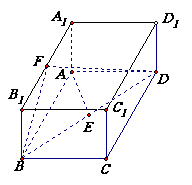
(I)求异面直线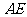 与
与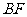 所成的角;
所成的角;
(II)求平面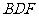 与平面
与平面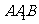 所成的二面角(锐角)的大小;
所成的二面角(锐角)的大小;
(III)求点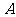 到平面
到平面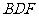 的距离.
的距离.
(21)(本小题满分12分)
已知数列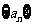 的首项
的首项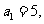 前
前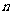 项和为
项和为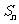 ,且
,且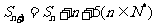 (n∈N*)
(n∈N*)
(I)证明数列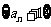 是等比数列;
是等比数列;
(II)令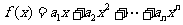 +…
+…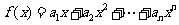 ,求函数
,求函数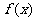 在点
在点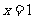 处的导数
处的导数 。
。
(22)(本小题满分14分)
已知动圆过定点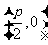 ,且与直线
,且与直线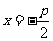 相切,其中
相切,其中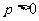 .
.
(I)求动圆圆心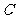 的轨迹的方程;
的轨迹的方程;
(II)设A、B是轨迹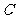 上异于原点
上异于原点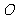 的两个不同点,直线
的两个不同点,直线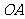 和
和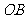 的倾斜角分别为
的倾斜角分别为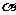 和
和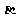 ,当
,当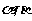 变化且
变化且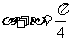 时,证明直线
时,证明直线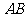 恒过定点,并求出该定点的坐标.
恒过定点,并求出该定点的坐标.
(13)某学校共有教师490人,其中不到40岁的有350人,40岁及以上的有140人。为了解普通话在该校教师中的推广普及情况,用分层抽样的方法,从全体教师中抽取一个样本容量为70人的样本进行普通话水平测试,其中在不到40岁的教师中应抽取的人数 。
(14)设双曲线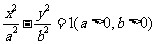 的右焦点为
的右焦点为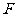 ,右准线
,右准线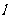 与两条渐近线交于P、
与两条渐近线交于P、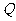 两点,如果
两点,如果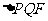 是直角三角形,则双曲线的离心率
是直角三角形,则双曲线的离心率 。
。
(15)设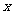 、
、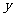 满足约束条件
满足约束条件 则使得目标函数
则使得目标函数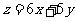 的最大的点
的最大的点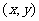 是 .
是 .
(16)已知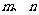 是不同的直线,
是不同的直线,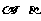 是不重合的平面,给出下列命题:
是不重合的平面,给出下列命题:
①若m∥α,则m平行于平面α内的任意一条直线
②若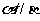 ,m
,m α,n
α,n β,则m∥n
β,则m∥n
③若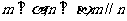 ,则
,则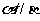
④若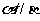 ,m
,m α,则m∥β
α,则m∥β
上面的命题中,真命题的序号是_____________(写出所有真命题的序号)
(1)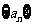 使首项
使首项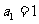 ,公差
,公差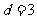 的等差数列,如果
的等差数列,如果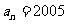 ,则序号
,则序号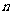 等于 ( )
等于 ( )
(A)667; (B)668; (C)669; (D)670
(2)下列大小关系正确的是
(A)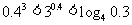 (B)
(B)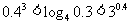
(C)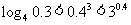 (D)
(D)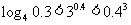
(3)函数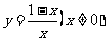 的反函数图像大致是
(
)
的反函数图像大致是
(
)
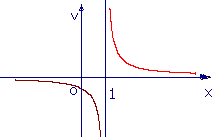
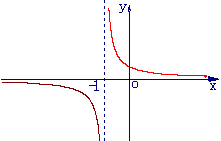
(A) (B)
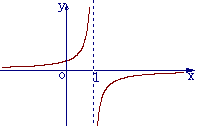
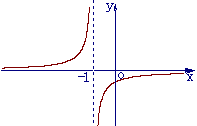
(C) (D)
(4)已知函数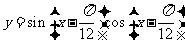 ,则下列判断正确的是
(
)
,则下列判断正确的是
(
)
(A)此函数的最小周期为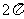 ,其图像的一个对称中心是
,其图像的一个对称中心是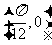
(B)此函数的最小周期为 ,其图像的一个对称中心是
,其图像的一个对称中心是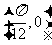
(C)此函数的最小周期为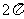 ,其图像的一个对称中心是
,其图像的一个对称中心是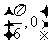
(D)此函数的最小周期为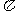 ,其图像的一个对称中心是
,其图像的一个对称中心是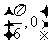
(5)下列函数既是奇函数,又在区间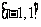 上单调递减的是
( )
上单调递减的是
( )
(A)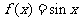 (B)
(B)
(C)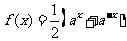 (D)
(D)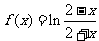
(6)如果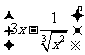 的展开式中各项系数之和为128,则展开式中
的展开式中各项系数之和为128,则展开式中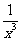 的系数是( )
的系数是( )
(A)7
(B) (C)21
(D)
(C)21
(D)
(7)函数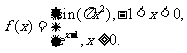 若
若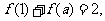 则
则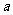 的所有可能值为
( )
的所有可能值为
( )
(A)1 (B)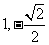 (C)
(C)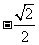 (D)
(D)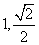
(8)已知向量a、b,且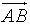 =a+2b,
=a+2b,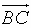 =-5a+6b,
=-5a+6b,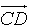 =7a-2b,则一定共线的三点是( )
=7a-2b,则一定共线的三点是( )
(A)A、B、D (B)A、B、C (C)B、C、D (D)A、C、D
(9)设地球的半径为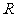 ,若甲地位于北纬
,若甲地位于北纬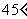 东经
东经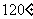 ,乙地位于南纬
,乙地位于南纬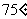 东经
东经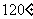 ,则甲、乙两地的球面距离为
( )
,则甲、乙两地的球面距离为
( )
(A)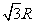 ; (B)
; (B)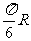 ; (C)
; (C)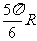 ; (D)
; (D)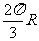
(10)10张奖券中只有3张有奖,5个人购买,每人1张,至少有1人中奖的概率是( )
(A)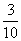 (B)
(B)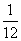 (C)
(C)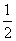 (D)
(D)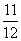
(11)设集合A、B是全集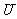 的两个子集,则A
的两个子集,则A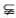 B是(CU A)∪B=
B是(CU A)∪B=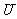 的( )
的( )
(A)充分不必要条件 (B)必要不充分条件
(C)充要条件 (D)既不充分也不必要条件
(12)设直线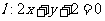 关于原点对称的直线为
关于原点对称的直线为 ,若
,若 与椭圆
与椭圆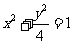 的交点为A、B,点
的交点为A、B,点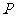 为椭圆上的动点,则使
为椭圆上的动点,则使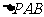 的面积为
的面积为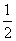 的点
的点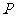 的个数为( )
的个数为( )
(A)1 (B)2 (C)3 (D)4
第II卷(共90分)
(17)(本小题满分12分)
设函数f(x)=2|x+1|-|x-1| ,求使f(x)≥2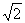 的x取值范围。
的x取值范围。
(18)(本小题满分12分)
已知{an}是各项均为正数的等差数列,lga1、lga2、lga4成等差数列,又bn= ,n=1,2,3….
,n=1,2,3….
(Ⅰ)证明{bn}为等比数列;
(Ⅱ)如果无穷等比数列{bn}各项的和S=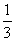 ,求数列{an}的首项a1和公差d.
,求数列{an}的首项a1和公差d.
(注:无穷数列各项的和即当n→∞时数列前n项和的极限)
(19)(本小题满分12分)
甲、乙两队进行一场排球比赛、根据以往经验,单局比赛甲队胜乙队的概率为0.6.本场比赛采用五局三胜制,即先胜三局的队获胜,比赛结束.设各局比赛相互间没有影响。令ξ为本场比赛的局数,求ξ的概率分布和数学期望。(精确0.0001)
(20)(本小题满分12分)
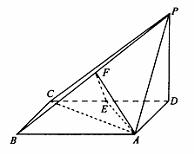
如图、四棱锥P-ABCD中,底面ABCD为矩形,PD⊥底面ABCD,AD=PD,E、F分别为CD、PB的中点。
(Ⅰ)求证:EF⊥平面PAB;
(Ⅱ)设AB=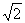 BC,求AC与平面AEF所成的角的大小。
BC,求AC与平面AEF所成的角的大小。
(21)(本小题满分14分)
P、Q、M、N四点都在椭圆x2+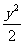 =1上,F为椭圆在y轴正半轴上的焦点.已知
=1上,F为椭圆在y轴正半轴上的焦点.已知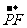 与
与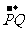 共线,
共线,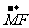 与
与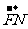 共线,且
共线,且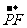 ·
·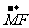 =0.求四边形PMQN的面积的最小值和最大值。
=0.求四边形PMQN的面积的最小值和最大值。
(22)(本小题满分12分)
已知a≥0,函数f(x)=(x2-2ax)ex.
(Ⅰ)当x为何值时,f(x)取得最小值?证明你的结论;
(Ⅱ)设f(x)在[-1,1]上是单调函数,求a的取值范围.
(13)圆心为(1,2)且与直线5x-12y-7=0相切的圆的方程为______________。
(14)设α为第四象限的角,若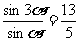 ,则tan2α=_______________。
,则tan2α=_______________。
(15)在由数字0,1,2,3,4,5所组成的没有重复数字的四位数中,不能被5整除的数共有_个。
(16)下面是关于三棱锥的四个命题:
① 底面是等边三角形,侧面与底面所成的二面角都相等的三棱锥是正三棱锥。
② 底面是等边三角形,侧面都是等腰三角形的三棱锥是正三棱锥。
③ 底面是等边三角形,侧面的面积都相等的三棱锥是正三棱锥。
④ 侧棱与底面所成的角都相等,且侧面与底面所成的二面角都相等的三棱锥是正三棱锥。其中,真命题的编号是_____________________.(写出所有真命题的编号)
(1)函数f(x)=|sinx+cosx|的最小正周期是
(A)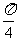 (B)
(B)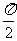 (C)π
(D)2π
(C)π
(D)2π
(2)正方体ABCD-A1B1C1D1中,P、Q、R分别是AB、AD、B1C1的中点。那么,正方体的过P、Q、R的截面图形是
(A)三角形 (B)四边形 (C)五边形 (D)六边形
(3)函数y=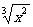 -1(x≤0)的反函数是
-1(x≤0)的反函数是
(A)y=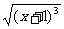 (x≥-1)
(B)y=-
(x≥-1)
(B)y=-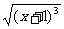 (x≥-1)
(x≥-1)
(C)y=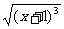 (x≥0)
(D)y=-
(x≥0)
(D)y=-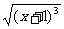 (x≥0)
(x≥0)
(4)已知函数y=tanωx在(-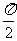 ,
,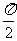 )内是减函数,则
)内是减函数,则
(A)0<ω≤1 (B)-1≤ω<0
(C)ω≥1 (D)ω≤-1
(5)设a、b、c、d∈R,若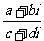 为实例,则
为实例,则
(A)bc+ad≠0 (B)bc-ad≠0
(C)bc-ad=0 (D)bc+ad=0
(6)已知双曲线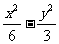 =1的焦点为F1、F2,点M在双曲线上且MF1⊥x轴,则F1到直线F2M的距离为
=1的焦点为F1、F2,点M在双曲线上且MF1⊥x轴,则F1到直线F2M的距离为
(A)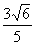 (B)
(B)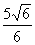 (C)
(C)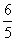 (D)
(D)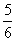
(7)锐角三角形的内角A、B满足tanA-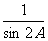 =tanB,则有
=tanB,则有
(A)sin2A-cosB=0 (B)sin2A+cosB=0
(C)sin2A-sinB=0 (D)sin2A+sinB=0起
(8)已知点A(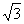 ,1),B(0,0),C(
,1),B(0,0),C(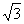 ,0)。设∠BAC的平分线AE与BC相交于E,
,0)。设∠BAC的平分线AE与BC相交于E,
那么有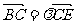 ,其中λ等于
,其中λ等于
(A)2
(B)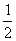 (C)-3
(D)-
(C)-3
(D)-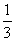
(9)已知集合M={x|x2-3x-28≤0},N={x|x2-x-6>0 },则M∩N为
(A){x|-4≤x<-2或3<x≤7} (B){x|-4<x≤-2或3≤x<7}
(C){x|x≤-2或x>3} (D){x|x<-2或x≥3}
(10)点P在平面上作匀速直线运动,速度向量v=(4,-3)(即点P的运动方向与v相同,且每秒移动的距离为|v|个单位),设开始时点P的坐标为(-10,10),则5秒后点P的坐标为
(A)(-2,4) (B)(-30,25) (C)(10,-5) (D)(5,-10)
(11)如果a1,a2,…a8为各项都大于零的等差数列,公差d≠0,则
(A)a1a8>a4a5 (B)a1a8<a4a5 (C)a1+a8>a4+a5 (D)a1a8=a4a5
(12)将半径都为1的4个钢球完全装入形状为正四面体的容器里,这个正四面体的高的最小值为
(A)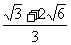 (B)2+
(B)2+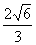 (C)
(C)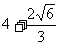 (D)
(D)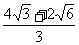
第Ⅱ卷
(17)设函数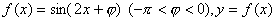 图像的一条对称轴是直线
图像的一条对称轴是直线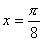 。
。
(Ⅰ)求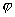 ;
;
(Ⅱ)求函数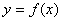 的单调增区间;
的单调增区间;
(Ⅲ)证明直线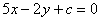 与函数
与函数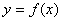 的图像不相切。
的图像不相切。
(18)已知四棱锥P-ABCD的底面为直角梯形,AB∥DC,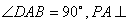 底面ABCD,且PA=AD=DC=
底面ABCD,且PA=AD=DC=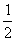 AB=1,M是PB的中点。
AB=1,M是PB的中点。
(Ⅰ)证明:面PAD⊥面PCD;
(Ⅱ)求AC与PB所成的角;
(Ⅲ)求面AMC与面BMC所成二面角的大小。
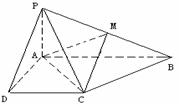
(19)设等比数列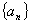 的公比为
的公比为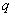 ,前n项和
,前n项和 。
。
(Ⅰ)求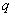 的取值范围;
的取值范围;
(Ⅱ)设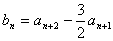 ,记
,记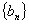 的前n项和为
的前n项和为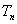 ,试比较
,试比较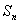 和
和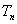 的大小。
的大小。
(20)9粒种子分种在3个坑内,每坑3粒,每粒种子发芽的概率为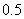 ,若一个坑内至少有1粒种子发芽,则这个坑不需要补种,若一个坑内的种子都没发芽,则这个坑需要补种。假定每个坑至多补种一次,每补种1个坑需10元,用ξ表示补种费用,写出ξ的分布列并求ξ的数学期望。(精确到
,若一个坑内至少有1粒种子发芽,则这个坑不需要补种,若一个坑内的种子都没发芽,则这个坑需要补种。假定每个坑至多补种一次,每补种1个坑需10元,用ξ表示补种费用,写出ξ的分布列并求ξ的数学期望。(精确到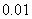 )
)
(21)已知椭圆的中心为坐标原点O,焦点在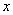 轴上,斜率为1且过椭圆右焦点F的直线交椭圆于A、B两点,
轴上,斜率为1且过椭圆右焦点F的直线交椭圆于A、B两点,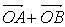 与a=(3,-1)共线。
与a=(3,-1)共线。
(Ⅰ)求椭圆的离心率;
(Ⅱ)设M为椭圆上任意一点,且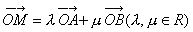 ,证明
,证明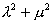 为定值。
为定值。
(22)(Ⅰ)设函数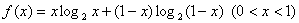 ,求
,求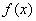 的最小值;
的最小值;
(Ⅱ)设正数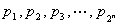 满足
满足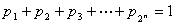 ,证明
,证明 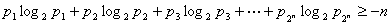 .
.
(13)若正整数m满足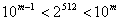 ,则m = 。
,则m = 。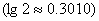
(14)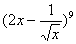 的展开式中,常数项为 。(用数字作答)
的展开式中,常数项为 。(用数字作答)
(15)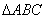 的外接圆的圆心为O,两条边上的高的交点为H,
的外接圆的圆心为O,两条边上的高的交点为H,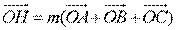 ,则实数m =
,则实数m =
(16)在正方形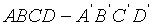 中,过对角线
中,过对角线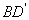 的一个平面交
的一个平面交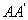 于E,交
于E,交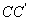 于F,则
于F,则
① 四边形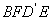 一定是平行四边形.
一定是平行四边形.
② 四边形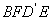 有可能是正方形.
有可能是正方形.
③ 四边形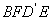 在底面ABCD内的投影一定是正方形.
在底面ABCD内的投影一定是正方形.
④ 平面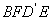 有可能垂直于平面
有可能垂直于平面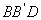 .
.
以上结论正确的为 。(写出所有正确结论的编号)
12.过三棱柱任意两个顶点的直线共15条,其中异面直线有
(A)18对 (B)24对
(C)30对 (D)36对
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com