
7.设双曲线的焦点在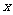 轴上,两条渐近线为
轴上,两条渐近线为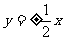 ,则该双曲线的离心率
,则该双曲线的离心率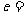 ( )
( )
A.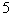 B.
B. 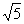 C.
C.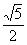 D.
D.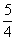
6.设复数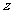 的辐角的主值为
的辐角的主值为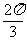 ,虚部为
,虚部为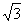 ,则
,则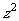 = ( )
= ( )
A.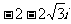 B.
B.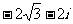 C.
C.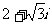 D.
D.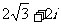
5.函数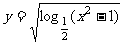 的定义域为 ( )
的定义域为 ( )
A.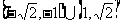 B.
B.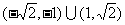
C.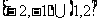 D.
D.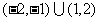
4.圆 在点
在点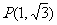 处的切线方程为 ( )
处的切线方程为 ( )
A.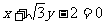 B.
B.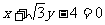
C.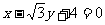 D.
D.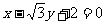
3.设数列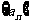 是等差数列,且
是等差数列,且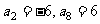 ,
,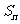 是数列
是数列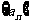 的前
的前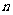 项和,则 ( )
项和,则 ( )
A.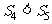 B.
B.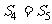 C.
C.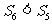 D.
D.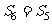
2.函数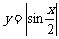 的最小正周期是 ( )
的最小正周期是 ( )
A. 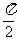 B.
B. 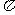 C.
C.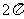 D.
D.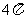
1.设集合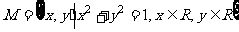 ,
,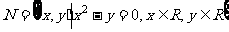 ,则集合
,则集合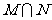 中元素的个数为 ( )
中元素的个数为 ( )
A.1 B.2 C.3 D.4
21.(本题满分18分)本题共有3个小题,第1小题满分4分,第2小题满分6分,第3小题满分8分.已知倾斜角为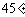 的直线
的直线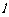 过点
过点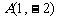 和点
和点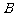 ,
,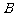 在第一象限,
在第一象限,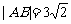 .
.
(1) 求点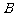 的坐标;
的坐标;
(2) 若直线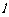 与双曲线
与双曲线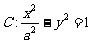
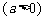 相交于
相交于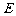 、
、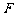 两点,且线段
两点,且线段 的中点坐标为
的中点坐标为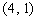 ,求
,求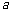 的值;
的值;
(3) 对于平面上任一点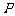 ,当点
,当点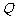 在线段
在线段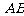 上运动时,称
上运动时,称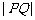 的最小值为
的最小值为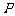 与线段
与线段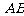 的距离. 已知点
的距离. 已知点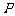 在
在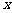 轴上运动,写出点
轴上运动,写出点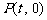 到线段
到线段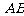 的距离
的距离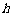 关于
关于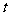 的函数关系式.
的函数关系式.
20.(本题满分16分)本题共有3个小题,第1小题满分4分,第2小题满分6分,第3小题满分6分.已知函数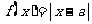 ,
,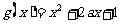 (
(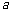 为正常数),且函数
为正常数),且函数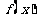 与
与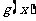 的图像在
的图像在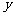 轴上的截距相等。
轴上的截距相等。
(1)求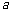 的值;
的值;
(2)求函数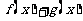 的单调递增区间;
的单调递增区间;
(3)若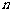 为正整数,证明:
为正整数,证明: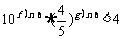 .
.
19. (本题满分14分) 本题共有2个小题,第一小题满分6分,第2小题满分8分.
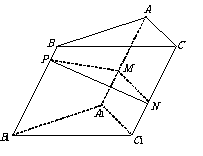
如图,点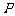 为斜三棱柱
为斜三棱柱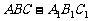 的侧棱
的侧棱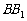 上一点,
上一点,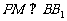 交
交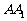 于点
于点 ,
, 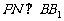 交
交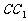 于点
于点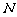 .
.
(1) 求证: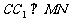 ;
;
(2) 在任意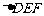 中有余弦定理:
中有余弦定理: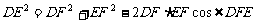 . 拓展到空间,类比三角形的余弦定理,写出斜三棱柱的三个侧面面积与其中两个侧面所成的二面角之间的关系式,并予以证明.
. 拓展到空间,类比三角形的余弦定理,写出斜三棱柱的三个侧面面积与其中两个侧面所成的二面角之间的关系式,并予以证明.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com