
有一项是符合题目要求的.
(1)满足条件M∪{1}={1,2,3}的集合M的个数是
(A)4 (B)3 (C)2 (D)1
(2)在平面直角坐标系中,已知两点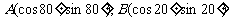 则|AB|的值是
则|AB|的值是
(A)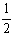 (B)
(B)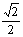 (C)
(C)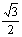 (D)1
(D)1
(3)下列四个函数中,以π为最小正周期,且在区间(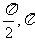 )上为减函数的是
)上为减函数的是
(A)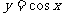 (B)
(B)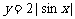 (C)
(C)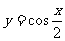 (D)
(D)
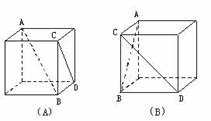
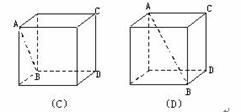
(4)在下列四个正方体中,能得出AB⊥CD的是
(5)64个直径都为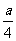 的球,记它们的体积之和为V甲,表面积之和为S甲;一个直径为a的球,记其体积为V乙,表面积为S乙,则
的球,记它们的体积之和为V甲,表面积之和为S甲;一个直径为a的球,记其体积为V乙,表面积为S乙,则
(A)V甲>V乙且S甲>S乙 (B)V甲<V乙且S甲<S乙
(C)V甲=V乙且S甲>S乙 (D)V甲=V乙且S甲=S乙
(6)若直线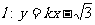 与直线
与直线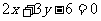 的交点位于第一象限,则直线l的倾斜角的取值范围
的交点位于第一象限,则直线l的倾斜角的取值范围
(A)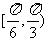 (B)
(B)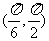 (C)
(C)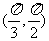 (D)
(D)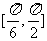
(7)(1+i)8等于
(A)16i (B)-16i (C)-16 (D)16
(8)若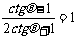 ,则
,则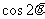 的值为
的值为
(A)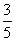 (B)-
(B)-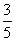 (C)
(C)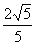 (D)-
(D)-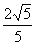
(9)5本不同的书,全部分给四个学生,每个学生至少1本,不同分法的种数为
(A)480 (B)240 (C)120 (D)96
(10)已知椭圆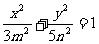 和双曲线
和双曲线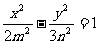 有公共的焦点,那么双曲线的渐近线方程是
有公共的焦点,那么双曲线的渐近线方程是
(A)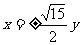 (B)
(B)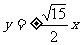 (C)
(C)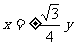 (D)
(D)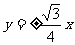
(11)已知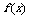 的定义在(0,3)上的函数,
的定义在(0,3)上的函数,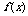 的图象如图所示,那么不等式
的图象如图所示,那么不等式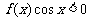
的解集是
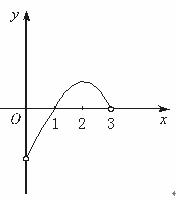
(A)(0,1)∪(2,3) (B)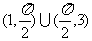
(C)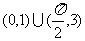 (D)
(D)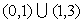
(12)如图所示,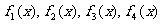 是定义在[0,1]上的四个函数,其中满足性质:“对[0,1]中任意的x1和x2,
是定义在[0,1]上的四个函数,其中满足性质:“对[0,1]中任意的x1和x2,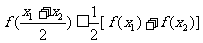 恒成立”的只有
恒成立”的只有
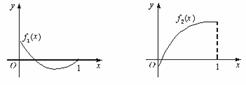
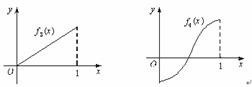
(A)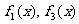 (B)
(B)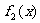 (C)
(C)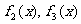 (D)
(D)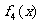
第Ⅱ卷
(17)(本小题满分12分)
已知 的值。
的值。
注意:考生在(18甲)、(18乙)两题中选一题作答,如果两题都答,只以(18甲)计分。
(18甲)(本小题满分12分)
如图,正三棱柱ABC-A1B1C1的底面边长为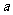 ,侧棱长为
,侧棱长为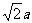 。
。
(Ⅰ)建立适当的坐标系,并写出点A、B、A1、C1的坐标;
(Ⅱ)求AC1与侧面ABB1A1所成的角

(18乙)如图,正方形ABCD、ABEF的边长都是1,而且平面ABCD、ABEF互相垂直。点M在AC上移动,点N在BF上移动,若CM=BN=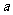
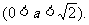
(Ⅰ)求MN的长;
(Ⅱ)当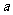 为何值时,MN的长最小;
为何值时,MN的长最小;
(Ⅲ)当MN长最小时,求面MNA与面MNB所成的二面角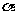 的大小。
的大小。

(19)(本小题满分12分)
某单位6个员工借助互联网开展工作,每个员工上网的概率都是0.5(相互独立)。
(Ⅰ)求至少3人同时上网的概率;
(Ⅱ)至少几人同时上网的概率小于0.3?
(20)(本小题满分12分)
已知 ,函数
,函数 。设
。设 ,记曲线
,记曲线 在点
在点 处的切线为
处的切线为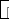 。
。
(Ⅰ)求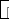 的方程;
的方程;
(Ⅱ)设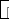 与
与 轴交点为
轴交点为 。证明:
。证明:
①  ;
;
② 若 ,则
,则
(21)(本小题满分12分)
已知两点M(-1,0),N(1,0),且点P使 成等差小于零的等差数列。
成等差小于零的等差数列。
(Ⅰ)点P的轨迹是什么曲线?
(Ⅱ)若点P坐标为 ,记
,记 为
为 与
与 的夹角,求
的夹角,求 。
。
(22)已知 是由非负整数组成的数列,满足
是由非负整数组成的数列,满足
 ……。
……。
(Ⅰ)求 ;
;
(Ⅱ)证明 ……;
……;
(Ⅲ)求 的通项公式及其前
的通项公式及其前 项和
项和 。
。
(13)函数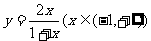 图象与其反函数图象的交点坐标为________。
图象与其反函数图象的交点坐标为________。
(14)椭圆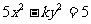 的一个焦点是(0,2),那么k=_____________.
的一个焦点是(0,2),那么k=_____________.
(15)直线x=0,y=0,x=2与曲线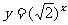 所围成的图形绕x轴旋转一周而成的旋转体的体积等于__________________。
所围成的图形绕x轴旋转一周而成的旋转体的体积等于__________________。
(16)已知函数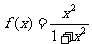 ,那么
,那么
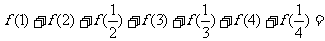 ______________。
______________。
(1)曲线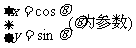 上的点到两坐标轴的距离之和的最大值是
上的点到两坐标轴的距离之和的最大值是
(A)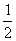 (B)
(B)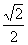 (C)1 (D)
(C)1 (D)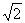
(2)复数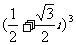 的值是
的值是
(A) (B)
(B)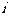 (C)
(C)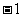 (D)1
(D)1
(3)已知m、n异面直线,
(A)与m、n都相交 (B)与m、n中至少一条相交
(B)与m、n都不相交 (D)至多与m、n中的一条相交
(4)不等式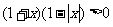 的解集是
的解集是
(A)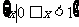 (B)
(B)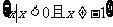
(C)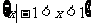 (D)
(D)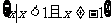
(5)在(0,2π)内,使sinx>cosx成立的x取值范围为
(A)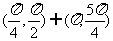 (B)
(B)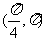
(C)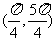 (D)
(D)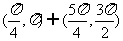
(6)设集合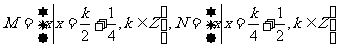 则
则
(A)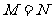 (B)
(B)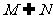 (C)
(C)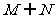 (D)
(D)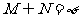
(7)正六棱柱ABCDEF-A1B1C1D1E1F1的底面边长为1,侧棱长为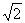 ,则这个棱柱的侧面对角线E1D独角戏与BC1所成的角是
,则这个棱柱的侧面对角线E1D独角戏与BC1所成的角是
(A)900 (B)600 (C)450 (D)300
(8)函数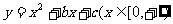 是单调函数的充要条件是
是单调函数的充要条件是
(A) b≥0 (B)b≤0 (C)b>0 (D)b<0
(9)已知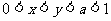 ,则有
,则有
(A)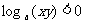 (B)
(B)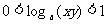
(C)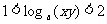 (D)
(D)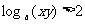
(10)平面直角坐标系中,O为坐标原点,已知两点A(3,1),B(-1,3),若点C满足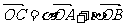 ,其中
,其中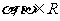 ,且
,且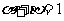 ,则点C的轨迹方程为:
,则点C的轨迹方程为:
(A) 3x-2y-11=0 (B)(x-1)2+(y-2)2=5
(C) 2x-y=0 (D)x+2y-5=0
(11)从正方体的6个面中选取3个面,其中有2个面不相邻的选法共有
(A) 8种 (B)12种 (C)16种 (D)20种
(12)据2002年3月5日九届人大五次会议《政府工作报告》:“2001年国内生产总值达到95933亿元,比上年增长7.3%。” 如果“十·五”期间(2001年-2005年)每年的国内生产总值都按此年增长率增长,那么到“十·五”末我国国内年生产总值约为
(A)115000亿元 (B)120000亿元 (C)127000亿元 (D)135000亿元
第Ⅱ卷
(15)(本小题满分13分)
已知函数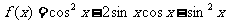 .
.
(Ⅰ)求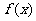 的最小正周期;
的最小正周期;
(Ⅱ)求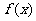 的最大值、最小值.
的最大值、最小值.
(16)(本小题满分13分)
已知数列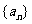 是等差数列,且
是等差数列,且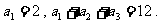
(Ⅰ)求数列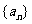 的通项公式;
的通项公式;
(Ⅱ)令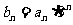 ,求数列
,求数列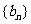 前n项和的公式.
前n项和的公式.
(17)(本小题满分15分)
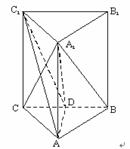
如图,正三棱柱ABC-A1B1C1中,D是BC的中点,AB=(A)
(Ⅰ)求证:A1D⊥B1C1;
(Ⅱ)求点D到平面ACC1的距离;
(Ⅲ)判断A1B与平面ADC1的位置关系,并证明你的结论.
(18)(本小题满分15分)
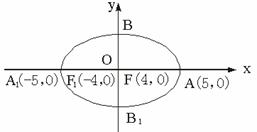
如图,A1、A为椭圆的两个顶点,F1、F2为椭圆的两个焦点.
(Ⅰ)写出椭圆的方程及其准线方程;
(Ⅱ)过线段OA上异于O,A的任一点K作OA的垂线,交椭圆于P,P1两点点,直线A1P与AP1交于点M.
求证:点M在双曲线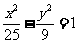 上.
上.
(19)(本小题满分14分)
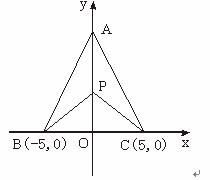
有三个新兴城镇,分别位于A,B,C三点处,且AB=AC=13km,BC=10km.今计划合建一个中心医院,为同时方便三镇,准备建在BC的垂直平分线上的P点处.(建立坐标系如图)
(Ⅰ)若希望点P到三镇距离的平方和为最小,点P应位于何处?
(Ⅱ)若希望点P到三镇的最远距离为最小,点P应位于何处?
(20)(本小题满分14分)
设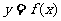 是定义在区间[-1,1]上的函数,且满足条件:
是定义在区间[-1,1]上的函数,且满足条件:
(ⅰ)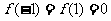 ;
;
(ⅱ)对任意的u,v∈[-1,1],都有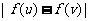 ≤
≤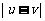 .
.
(Ⅰ)证明:对任意的x∈[-1,1],都有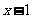 ≤
≤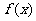 ≤
≤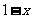 ;
;
(Ⅱ)判断函数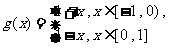 是否满足题设条件;
是否满足题设条件;
(Ⅲ)在区间[-1,1]上是否存在满足题设条件的函数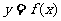 ,且使得对任意的u,
,且使得对任意的u,
v∈[-1,1],都有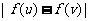 =
=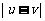 .
.
若存在,请举一例;若不存在,请说明理由.
(11)已知某球体的体积与其表面积的数值相等,则此球体的半径为______________.
(12)函数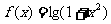 ,
,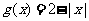 ,
,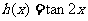 中,_____________是偶函数.
中,_____________是偶函数.
(13)以双曲线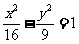 的右顶点为顶点,左焦点为焦点的抛物线的方程是______________.
的右顶点为顶点,左焦点为焦点的抛物线的方程是______________.
(14)将长度为1的铁丝分成两段,分别围成一个正方形和一个圆形,要使正方形与圆的面积之和最小,正方形的周长应为______________.
(1)设集合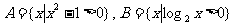 ,则A∩B等于
,则A∩B等于
(A)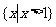 (B)
(B)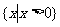
(C)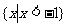 (D)
(D)
(2)设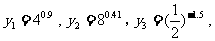 则
则
(A)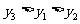 (B)
(B)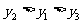
(C)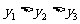 (D)
(D)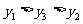
(3)“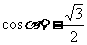 ”是“
”是“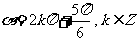 ”的
”的
(A)必要非充分条件 (B)充分非必要条件
(C)充分必要条件 (D)既非充分又非必要条件
(4)已知、是平面,m、n是直线.下列命题中不正确的是
(A)若m∥,∩=n,则m∥n
(B)若m∥n,m⊥,则n⊥
(C)若m⊥,m⊥,则∥
(D)若m⊥,m,则⊥
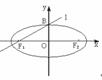
(5)如图,直线l: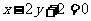 过椭圆的左焦点F1和一个顶点B该椭圆的离心率为
过椭圆的左焦点F1和一个顶点B该椭圆的离心率为
(A)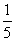 B)
B)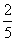 (C)
(C)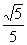 (D)
(D)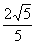
(6)若z∈C且|z+2-2i|=1,则|z-2-2i|的最小值是
(A)2 (B)3 (C)4 (D)5
(7)如果圆台的母线与底面成60°角,那么这个圆台的侧面积与轴截面面积的比为
(A)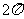 (B)
(B)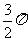 (C)
(C)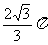 (D)
(D)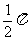
(8)若数列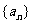 的通项公式是
的通项公式是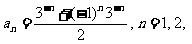 …,则
…,则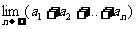 等于
等于
(A)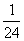 (B)
(B)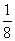 (C)
(C)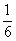 (D)
(D)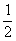
(9)从黄瓜、白菜、油菜、扁豆4种蔬菜品种中选出3种,分别种在不同土质的三块土地上,其中黄瓜必须种植,不同的种植方法共有
(A)24种 (B)18种 (C)12种 (D)6种
(10)某班试用电子投票系统选举班干部候选人,全班k名同学都有选举权和被选举权,他们的编号分别为1,2,…,k.规定:同意按“1”,不同意(含弃权)按“0”.令

其中i=1,2,…,k.且j=1,2,…,k.则同时同意第1,2号同学当选的人数为
(A)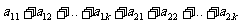
(B)
(C)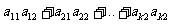
(D)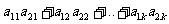
第Ⅱ卷
(17)(本小题满分12分)
已知函数f(x)=2sin x (sin x+cos x).
(Ⅰ)求函数f(x)的最小正周期和最大值;
(Ⅱ)在给出的直角坐标系中,画出函数y=f(x)的区间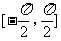 上的图象
上的图象

(18)(本小题满分12分)
如图,在直三棱柱ABC-A1B1C1中,底面是等腰直角三角形,∠ACB=90°,侧棱 AA1=2,D、E分别是CC1与A1B的中点,点E在平面ABD上的射影是△ABD的重心G.
(Ⅰ)求A1B与平面ABD所成角的大小(结果用反三角函数值表示);
(Ⅱ)求点A1到平面AED的距离.
(19)(本小题满分12分)
设a>0,求函数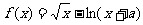 (x∈(0,+∞))的单调区间.
(x∈(0,+∞))的单调区间.
(20)(本小题满分12分)
A、B两个代表队进行乒乓球对抗赛,每队三名队员,A队队员是A1,A2,A3,B队队员是B1,B2,B3,按以往多次比赛的统计,对阵队员之间胜负概率如下:
|
对阵对员 |
A队队员胜的概率 |
A队队员负的概率 |
|
A1对B1 |
 |
 |
|
A2对B2 |
 |
 |
|
A3对B3 |
 |
 |
现按表中对阵方式出场,每场胜队得1分,负队得0分,设A队、B队最后所得总分分别为、
(Ⅰ)求、的概率分布;
(Ⅱ)求E、E.
(21)(本小题满分12分)
已知常数a>0,向量c=(0,a),i=(1,0).经过原点O以c+i为方向向量的直线与经过定点A(0,a)以i-2c为方向向量的直线相交于点P,其中∈R.试问:是否存在两个定点E、F,使得| PE | + | PF |为定值.若存在,求出E、F的坐标;若不存在,说明理由.
(22)(本小题满分14分)
设a0为常数,且an=3n-1-2an-1(n∈N).
(Ⅰ)证明对任意n≥1, ;
;
(Ⅱ)假设对任意n≥1有an>an-1,求a0的取值范围.
(13)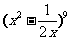 展开式中x9的系数是
.
展开式中x9的系数是
.
(14)某公司生产三种型号的轿车,产量分别为1200辆,6000辆和2000辆,为检验该公司的产品质量,现用分层抽样的方法抽取46辆进行检验,这三种型号的轿车依次应抽取_______,_______,_________辆.
(15)某城市在中心广场建造一个花圃,花圃分为6个部分(如图),现要栽种4种不同颜色的花,每部分栽种一种且相邻部分不能栽种同样颜色的花,不同的栽种方法有_____种.(以数字作答)

(16)下列五个正方体图形中,l是正方体的一条对角线,点M、N、P分别为其所在棱的中点,能得出l⊥面MNP的图形的序号是 .(写出所有符合要求的图表序号)

(1)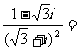
(A)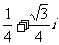 (B)
(B)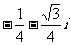
(C)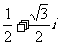 (D)
(D)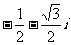
(2)已知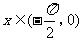 ,
,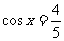 ,则tan 2x=
,则tan 2x=
(A)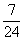 (B)
(B)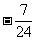
(C)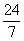 (D)
(D)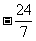
(3)设函数 若f(x0)>1,则x0的取值范围是
若f(x0)>1,则x0的取值范围是
(A)(-1,1) (B)(-1,+∞)
(C)(-∞,-2)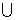 (0,+∞) (D)(-∞,-1)
(0,+∞) (D)(-∞,-1)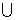 (1,+∞)
(1,+∞)
(4)O是平面上一定点,A、B、C是平面上不共线的三个点,动点P满足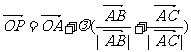 ,
,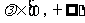 ,则P的轨迹一定通过△ABC的
,则P的轨迹一定通过△ABC的
(A)外心 (B)内心
(C)重心 (D)垂心
(5)函数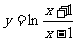 ,x∈(1,+∞)的反函数为
,x∈(1,+∞)的反函数为
(A)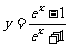 ,x∈(1,+∞) (B)
,x∈(1,+∞) (B)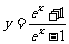 ,x∈(1,+∞)
,x∈(1,+∞)
(C)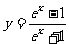 ,x∈(-∞,0) (D)
,x∈(-∞,0) (D)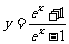 ,x∈(-∞,0)
,x∈(-∞,0)
(6)棱长为a的正方体中,连结相邻面的中心,以这些线段为棱的八面体的体积为
(A)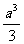 (B)
(B)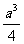 (C)
(C)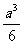 (D)
(D)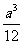
(7)设a>0,f(x)=ax2+bx+c,曲线y=f(x)在点P(x0,f(x0))处切线的倾斜角的取值范围为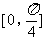 ,则P到曲线y=f(x)对称轴距离的取值范围为
,则P到曲线y=f(x)对称轴距离的取值范围为
(A)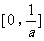 (B)
(B)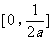
(C)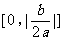 (D)
(D)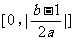
(8)已知方程(x2-2x+m)(x2-2x+n)的四个根组成一个首项为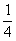 的等差数列,则
|m-n|=
的等差数列,则
|m-n|=
(A)1 (B)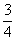 (C)
(C)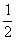 (D)
(D)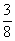
(9)已知双曲线中心在原点且一个焦点为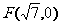 ,直线
,直线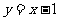 与其相交于M、N两点,MN中点的横坐标为
与其相交于M、N两点,MN中点的横坐标为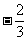 ,则此双曲线的方程是
,则此双曲线的方程是
(A)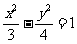 (B)
(B)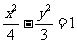
(C)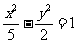 (D)
(D)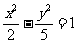
(10)已知长方形的四个顶点A(0,0),B(2,0),C(2,1)和D(0,1),一质点从AB的中点P0沿与AB夹角为θ的方向射到BC上的点P1后,依次反射CD、DA到AB和上的点P2、P3和P4(入射角等于反射角).设P4的坐标为(x4,0).若1< x4<2,则tgθ的取值范围是
(A)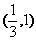 (B)
(B)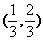
(C)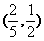 (D)
(D)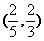
(11)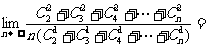
(A)3 (B)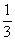 (C)
(C)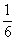 (D)6
(D)6
(12)一个四面体的所有棱长都为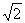 ,四个顶点在同一球面上,则此球的表面积为
,四个顶点在同一球面上,则此球的表面积为
(A)3 (B)4 (C)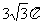 (D)6π
(D)6π
第Ⅱ卷
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com