
2.已知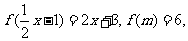 则
则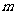 等于
等于
(A)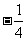 (B)
(B)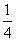 (C)
(C)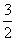 (D)
(D)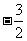
1.设函数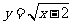 的定义域为集合M,集合N=
的定义域为集合M,集合N=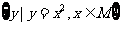 ,则
,则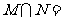
A.M B.N C.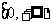 D.
D.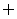
21. (本小题满分14分)
设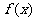 是定义在[-1,1]上的偶函数,
是定义在[-1,1]上的偶函数,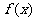 ,
,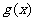 的图象关于直线
的图象关于直线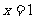 对称,且当x
对称,且当x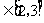 时,
时,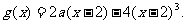
(1)求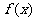 的表达式;
的表达式;
(2)是否存在正实数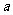 ,使函数
,使函数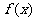 的图象的最高点在直线
的图象的最高点在直线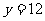 上,若存在,求出正实数
上,若存在,求出正实数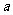 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
20. (本小题满分14分)
函数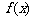 的定义域为R,并满足以下条件:
的定义域为R,并满足以下条件:
①对任意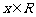 ,有
,有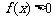 ;②对任意
;②对任意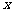 、
、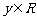 ,有
,有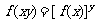 ;③
;③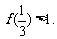
(Ⅰ)求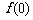 的值;
的值;
(Ⅱ)求证: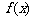 在R上是单调增函数;
在R上是单调增函数;
(Ⅲ)若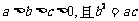 ,求证:
,求证: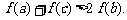
19. (本小题满分14分)
统计表明,某种型号的汽车在匀速行驶中每小时耗油量y(升)关于行驶速度x(千米/小时)的函数解析式可以表示为:y=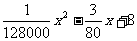 (0<x≤120).已知甲、乙两地相距100千米。
(0<x≤120).已知甲、乙两地相距100千米。
(Ⅰ)当汽车以40千米/小时的速度匀速行驶时,从甲地到乙地要耗油多少升?
(Ⅱ)当汽车以多大的速度匀速行驶时,从甲地到乙地耗油最少?最少为多少升?
18. (本小题满分14分)
已知f (x)=x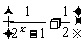 ,
,
(1) 证明:f (x)>0;
(2) 设F(x)=f(x+t)-f (x-t) (t≠o),试判断F(x)的奇偶性。
17.(本小题满分12分)
若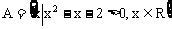 ,
,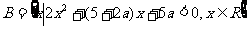 ,
,
且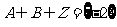 ,其中Z为整数集,求实数
,其中Z为整数集,求实数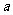 的取值范围。
的取值范围。
16.(本小题满分12分)
已知函数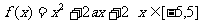
(1)当a=-1时,求函数f (x)的最大值和最小值.
(2)求实数a的取值范围,使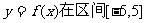 上是单调函数.
上是单调函数.
15. 对于函数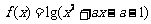 ,给出下列命题:①f (x)有最小值;②当a=0时,f (x)的值域为R;③当a>0时,f (x)在区间
,给出下列命题:①f (x)有最小值;②当a=0时,f (x)的值域为R;③当a>0时,f (x)在区间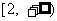 上有反函数;④若f (x)在区间
上有反函数;④若f (x)在区间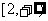 上是增函数,则实数a的取值范围是
上是增函数,则实数a的取值范围是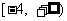 . 上述命题中正确的是
. 上述命题中正确的是
(填上所有正确命题序号) .
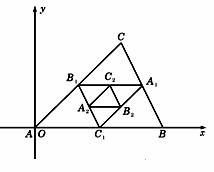
14. 如图,连结△ABC的各边中点得到一个新的△A1B1C1,又连结的△A1B1C1各边中点得到,如此无限继续下去,得到一系列三角形:△ABC,△A1B1C1,△A2B2C2,…,这一系列三角形趋向于一个点M,已知A(0,0) ,B(3,0),C(2,2),则点M的坐标是 .
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com