
9.函数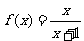 的递增区间为
。
的递增区间为
。
8.现定义: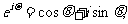 其中i为虚数单位,e为自然对数的底,
其中i为虚数单位,e为自然对数的底,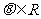 ,且实数指数幂的运算性质对
,且实数指数幂的运算性质对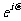 都适用,若
都适用,若
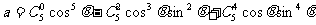
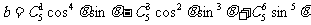 ,那么复数
,那么复数 等于 ( )
等于 ( )
A. B.
B.
C. D.
D.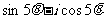
7.已知定义在R上 的偶函数f(x)的单调递减区间为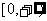 ,则不等式
,则不等式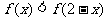 的解集是 ( )
的解集是 ( )
A.(1,2) B.(1,+∞) C.(2,+∞) D.(-∞,1)
5.若l、m为空间两条不同的直线,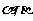 为空间两个不同的平面,则l⊥
为空间两个不同的平面,则l⊥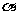 的一个充分条件是 ( )
的一个充分条件是 ( )
A.l∥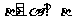 B.
B.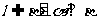
C.
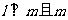 ∥
∥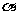 D.
D.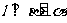 ∥
∥
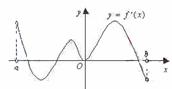 6.函数f(x)的定义域为开区间(a,b),导函数f‘(x)在(a,b)内的图象如图所示,则函数f(x)在开区间(a,b)内有极值点 ( )
6.函数f(x)的定义域为开区间(a,b),导函数f‘(x)在(a,b)内的图象如图所示,则函数f(x)在开区间(a,b)内有极值点 ( )
A.1个
B.2个
C.3个
D.4个
4.短轴长为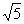 ,离心率
,离心率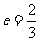 的椭圆两焦点为F1,F2,过F1作直线交椭圆于A、B两点,则△ABF2的周长为 ( )
的椭圆两焦点为F1,F2,过F1作直线交椭圆于A、B两点,则△ABF2的周长为 ( )
A.3 B.6 C.12 D.24
3.已知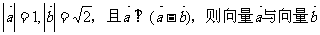 的夹角是 ( )
的夹角是 ( )
A.30° B.45° C.90° D.135°
2.为了了解某地区高三学生的身体发育情况,抽查了该地区100名年龄为17.5-18岁的男生体重(㎏),得到频率分布直方图如下:
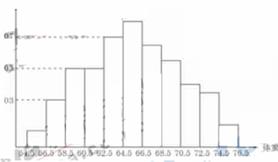
根据上图可得这100名学生中体重在(56.5,64.5)的学生人数是 ( )
A.20 B.30 C.40 D.50
1.已知集合A=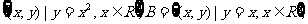 则A∩B的元素个数
则A∩B的元素个数
为 ( )
A.0个 B.1个 C.2个 D.无穷多个
22、(本题满分14分)
设函数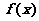 的定义域为R,当
的定义域为R,当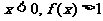 ,且对任意的实数
,且对任意的实数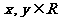 ,有
,有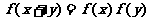
(1)求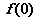 判断并证明函数
判断并证明函数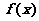 的单调性
的单调性
(2)数列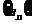 满足
满足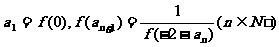
1求数列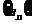 的通项公式
的通项公式
2令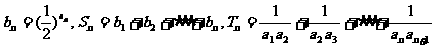 ,试比较
,试比较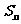 与
与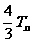 的大小,并加以证明;
的大小,并加以证明;
3当 时,不等式
时,不等式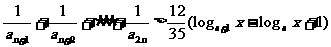 对于不小于2的正整数
对于不小于2的正整数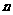 恒成立,求
恒成立,求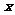 的取值范围。
的取值范围。
21、(本题满分12分)
有一种零存整取的储蓄项目,它是每月某日存入一笔相同金额,这是零存;到一定的时期到期,可以提出全部本金和利息,这是整取。它的本利和共识如下:
本利和=每期存入的金额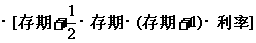
(1)试解释这个本利和公式
(2)若每月初存入100元,每月的利率为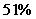 ,到第12个月底的本利和是多少?
,到第12个月底的本利和是多少?
(3)若每月初存入一笔金额,月利率是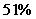 ,希望到第12个月底取得本利和2000元,那么每月初应存入多少金额?
,希望到第12个月底取得本利和2000元,那么每月初应存入多少金额?
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com