
1、函数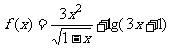 的定义域是
的定义域是
A.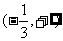 B.
B. 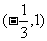 C.
C. 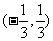 D.
D.
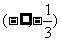
22.(文科做)已知函数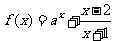
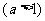 ,
,
求证:(1)函数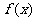 在
在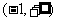 上为增函数;(2)方程
上为增函数;(2)方程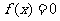 没有负数根.
没有负数根.
(理科做)已知数列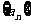 的前
的前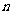 项的和为
项的和为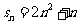 ,
,
(1)求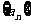 的通项公式;
的通项公式;
(2)设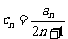 ,试判断并说明
,试判断并说明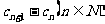 的符号;
的符号;
(3)设函数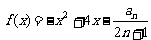 ,是否存在最大的实数
,是否存在最大的实数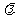 ,当
,当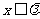 时,对于一切自然数
时,对于一切自然数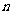 ,都有
,都有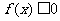 。
。
(4)已知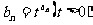 ,数列
,数列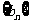 的前
的前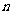 项为
项为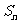 ,求
,求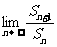 的值。
的值。
21.(文科做)已知函数f(x)=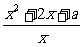 ,x∈[1,+∞
,x∈[1,+∞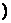 .
.
(1)当a=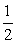 时,求函数f(x)的最小值;
时,求函数f(x)的最小值;
(2)若对任意x∈[1,+∞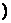 ,f(x)>0恒成立,试求实数a的取值范围.
,f(x)>0恒成立,试求实数a的取值范围.
(理科做)函数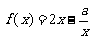 的定义域为
的定义域为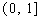 (
(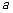 为实数).
为实数).
(1)当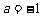 时,求函数
时,求函数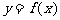 的值域;
的值域;
(2)若函数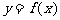 在定义域上是减函数,求
在定义域上是减函数,求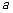 的取值范围;
的取值范围;
(3)求函数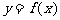 在
在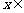
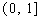 上的最大值及最小值,并求出函数取最值时
上的最大值及最小值,并求出函数取最值时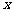 的值.
的值.
20.某城市自来水厂蓄水池现有水9千吨,水厂每小时向池中注水2千吨,同时向全市供水,x小时内供水总量为8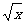 千吨,问:
千吨,问:
(1) 多少小时后,蓄水池内水量最少?
(2) 当蓄水池水量少于3千吨时,供水会出现紧张现象,现决定扩大生产,每小时向池内注水3千吨,能否消除供水紧张现象,为什么?
19. 已知函数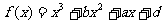 的图象过点P(0,2),且在点M
的图象过点P(0,2),且在点M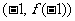 处的切线方程为
处的切线方程为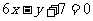 .
.
(Ⅰ)求函数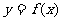 的解析式;
的解析式;
(Ⅱ)求函数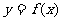 的单调区间.
的单调区间.
18. 设命题p:函数f(x)= 是R上的减函数,命题q:函数
是R上的减函数,命题q:函数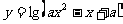 的定义域为R,如果“(非p)或q”为假命题,求实数a的取值范围。
的定义域为R,如果“(非p)或q”为假命题,求实数a的取值范围。
17. 设数列 的前n项和为Sn=2n2,
的前n项和为Sn=2n2,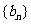 为等比数列,且
为等比数列,且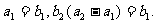
求数列 和
和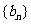 的通项公式;
的通项公式;
16.设函数f(x)=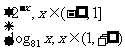 ,则满足f(x)=
,则满足f(x)=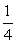 的x值为 .
的x值为 .
15.已知数列 中,
中,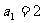 ,且
,且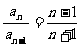 ,则
,则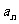 =________________.
=________________.
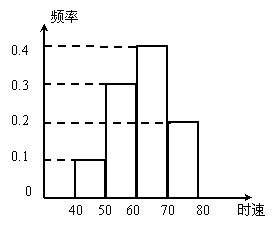
14.(文科做)200辆汽车通过某一段公路时的时速频率分布直方图如图所示,则时速在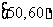 的汽车大约有
辆。
的汽车大约有
辆。
(理科做)极限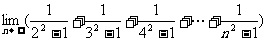 的值是
的值是
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com