
4.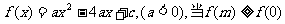 时,实数m满足的范围 ( )
时,实数m满足的范围 ( )
A.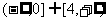 B.(0,+∞)
B.(0,+∞)
C.(0,4) D.[0,4]
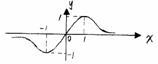 5.
5.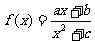 的图象如右图所示,则a,b,c三实数满足的关系是 ( )
的图象如右图所示,则a,b,c三实数满足的关系是 ( )
A.a>c>b B.a>b>c
C.b>a>c D.a,b,c大小不定
2.不等式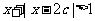 的解集为R时,实数c满足条件 ( )
的解集为R时,实数c满足条件 ( )
A.c<1 B.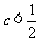 C.
C.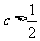 D.c>1
D.c>1
 3.
3.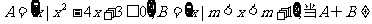 时,实数m满足( )
时,实数m满足( )
A.m<0 B.m<3 C.0≤m<3 D.0<m<3
1.如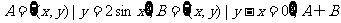 的子集数为 ( )
的子集数为 ( )
A.2个 B.4个 C.8个 D.8个以上
22.已知二次函数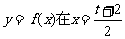 处取得最小值
处取得最小值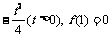
(1)求y = f (x)的表达式;
(2)若任意实数x都满足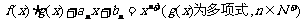 ,试用t表示an和bn;
,试用t表示an和bn;
(3)设圆Cn的方程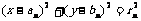 ,圆Cn与Cn+1外切(n = 1,2,3,…),{rn}是各项都是正数的等比数列,记Sn为前n个圆的面积之和,求rn,Sn.
,圆Cn与Cn+1外切(n = 1,2,3,…),{rn}是各项都是正数的等比数列,记Sn为前n个圆的面积之和,求rn,Sn.
21.设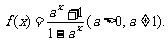
(1)求f (x)的反函数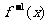 ;
;
(2)讨论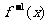 在(1,+∞)上的单调性,并加以证明;
在(1,+∞)上的单调性,并加以证明;
(只理科做)(3)令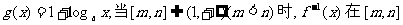 上的值域是
上的值域是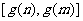 ,求a的取值范围.
,求a的取值范围.
20.(本小题满分12分)
通过研究学生的学习行为,心理学家发现,学生的接受能力依赖于教师引入概念和描述问题所用的时间。讲座开始时,学生的兴趣激增;中间有一段不太长的时间,学生的兴趣保持较理想的状态,随后学生的注意力开始分散,分析结果和实验表明,用f (x)表示学生掌握和接受概念的能力,x表示提出概念和讲授概念的时间(单位:分),可有以下的公式: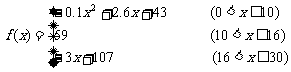
(1)开讲多少分钟,学生的接受能力最强?能维持多少时间?
(2)开讲5分钟与开讲20分钟比较,学生的接写能力何时强一些?
(3)一个数学题,需要55的接受能力以及13分钟时间,老师能否及时在学生一直达到所需接受能力状态下讲授完这个难题?
19.(本小题满分12分)
已知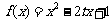 ,其定义域为
,其定义域为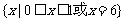 ,
,
(1)当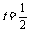 时,求函数f (x)的值域;
时,求函数f (x)的值域;
(2)当f (x)在定义域内有反函数时,求t的取值范围.
18.(本小题满分12分)
已知: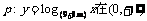 上是增函数,q:方程
上是增函数,q:方程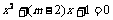 有两个正根,若p与q有且只有一个正确,求实数m的取值范围.
有两个正根,若p与q有且只有一个正确,求实数m的取值范围.
17.(本小题满分12分)
设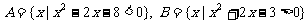 ,若
,若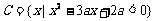 ,试求实数a的取值范围,使
,试求实数a的取值范围,使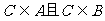 .
.
16.关于函数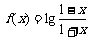 ,有下列五个命题:
,有下列五个命题:
①对定义域内任意x都有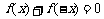 ;
;
②f (x)在(-1,1)上是减函数;
③函数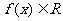 ;
;
④对于任意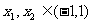 ,都有
,都有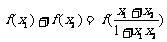 ;
;
⑤函数f (x)的图象关于点(-1,-1)对称,
其中正确命题的序号是 。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com