
3.命题p:不等式|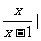 >
>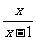 的解集为{x|0<x<1};命题q:在△ABC中,“A>B”是 “sinA>sinB”成立的必要非充分条件,则txjy
的解集为{x|0<x<1};命题q:在△ABC中,“A>B”是 “sinA>sinB”成立的必要非充分条件,则txjy
A.p真q假 B.“p且q”为真 C.“p或q”为假 D.p假q真
2.在等差数列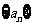 中,若
中,若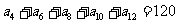 ,则
,则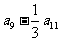 的值为
的值为
A.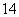 B.
B.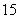 C.
C.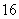 D.
D.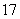
1.已知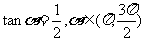 ,则
,则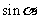 的值是
的值是
A.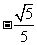 B.
B.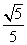 C.
C. 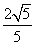 D.
D.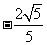
(17)(本小题满分12分)
(理)解关于x的不等式: ,(a>0且a≠1).
,(a>0且a≠1).
(文)解关于x的不等式: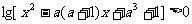 ,(a>0且a≠1).
,(a>0且a≠1).
(18)(本小题满分12分)
已知z1=3+4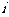 ,z2=65
,z2=65
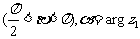 且
且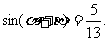
(Ⅰ)求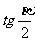 ;
;
(Ⅱ)设z1、z2在复平面内所对应点分别为P、Q、O为坐标原点,以OP、OQ为边作
平行四边形OPRQ,求对角线OR的长及平行四边形OPRQ的面积.
(19)(本小题满分12分)
如图,已知四棱锥P-ABCD的侧面PAD与底面ABCD垂直,△PAD是边长为a的正三角形,ABCD为直角梯形, AB//CD,DC=2a,∠ADC=90°,∠DCB=45°,E为BP中
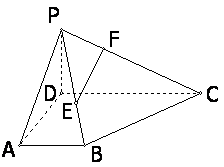 点,F在PC上且PF=
点,F在PC上且PF=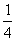 PC.
PC.
(Ⅰ)求证EF//平面PAD;
(Ⅱ)求三棱锥E-PCD的体积.
(20)(本小题满分12分,文科做(Ⅰ)、(Ⅱ),理科全做)
已知奇函数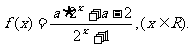
(Ⅰ)试确定实数a的值,并证明f(x)为R上的增函数;
(Ⅱ)记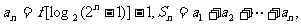 求
求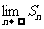 ;
;
(Ⅲ)若方程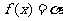 在(-∞,0)上有解,试证
在(-∞,0)上有解,试证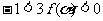 .
.
(21)(本小题满分12分)
某公司按现有能力,每月收入为70万元,公司分析部门测算,若不进行改革,入世后因竞争加剧收入将逐月减少.分析测算得入世第一个月收入将减少3万元,以后逐月多减少2万元,如果进行改革,即投入技术改造300万元,且入世后每月再投入1万元进行员工培训,则测算得自入世后第一个月起累计收入Tn与时间n(以月为单位)的关系为Tn=an+b,且入世第一个月时收入将为90万元,第二个月时累计收入为170万元,问入世后经过几个月,该公司改革后的累计纯收入高于不改革时的累计纯收入.
(22)(本小题满分14分,文科只做(Ⅰ)、(Ⅱ),理科全做)
已知抛物线C: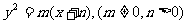 的焦点为原点,C的准线与直线
的焦点为原点,C的准线与直线
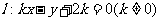 的交点M在x轴上,
的交点M在x轴上,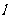 与C交于不同的两点A、B,线段AB的垂直平分线交x轴于点N(p,0).
与C交于不同的两点A、B,线段AB的垂直平分线交x轴于点N(p,0).
(Ⅰ)求抛物线C的方程;
(Ⅱ)求实数p的取值范围;
(Ⅲ)若C的焦点和准线为椭圆Q的一个焦点和一条准线,试求Q的短轴的端点的轨迹方程.
21.(本小题满分15分)
已知数列{an}的首项为a1=2,前n项和为Sn,且对任意的n∈N+,n≥2,an总是
3Sn-4与2-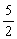 Sn-1的等差中项.
(1)求证:数列{an}是等比数列,并求通项an;
(2)若
Sn-1的等差中项.
(1)求证:数列{an}是等比数列,并求通项an;
(2)若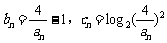 ,Tn、Rn分别为{bn}、{cn}的前n项和.问:是否存在正整数n,使得Tn>Rn,若存在,请求出所有n的值,否则请说明理由。
,Tn、Rn分别为{bn}、{cn}的前n项和.问:是否存在正整数n,使得Tn>Rn,若存在,请求出所有n的值,否则请说明理由。
20.(本小题满分15分)
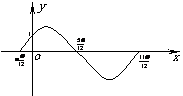 函数
函数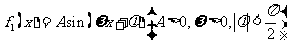 的一段图象过点
的一段图象过点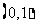 ,如图所示。
,如图所示。
⑴ 求函数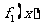 的解析式;
的解析式;
⑵ 将函数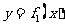 的图象向右平移
的图象向右平移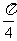 ,得到函数
,得到函数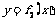 求
求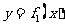
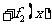 的最大值,并求此时自变量
的最大值,并求此时自变量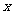 的集合。
的集合。
19.(本小题满分14分)
在等差数列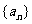 中,首项
中,首项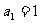 ,数列
,数列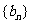 满足
满足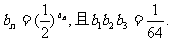
(1)求数列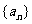 的通项公式;
的通项公式;
(2)求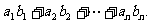
18.(本小题满分14分)
设函数f(x)=2cos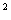 x+
x+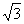 sin2x ,x∈R.
sin2x ,x∈R.
(1) 求f(x)的单调区间;
(2) 在△ABC中,a、b、c分别是角A、B、C的对边,f(A)=2,a=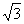 ,b+c=3(b>c),求b、c的长.
,b+c=3(b>c),求b、c的长.
17.(本小题满分12分)
已知集合M=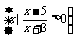 ,N={
,N={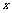 |(
|(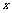 -3a)(
-3a)( 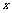 +2a)<0},若使M∩N=
+2a)<0},若使M∩N=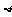 ,求a的取值范围。
,求a的取值范围。
16、给出下列五个命题:①不等式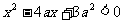 的解集为
的解集为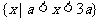 ;
;
②若函数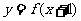 为偶函数,则
为偶函数,则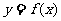 的图象关于
的图象关于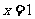 对称;
对称;
③若不等式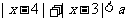 的解集为空集,必有
的解集为空集,必有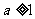 ;
;
④函数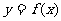 的图像与直线
的图像与直线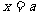 至多有一个交点;
至多有一个交点;
⑤若角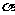 ,β满足cos
,β满足cos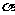 ·cos
·cos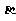 =1,则
=1,则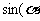 +
+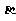 )=0.
)=0.
其中所有正确命题的序号是
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com