
7.对于函数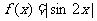 有下列命题 ( )
有下列命题 ( )
①函数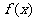 的最小正周期是
的最小正周期是 ;
;
②函数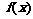 是偶函数;
是偶函数;
③函数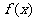 的图象关于直线
的图象关于直线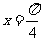 对称;
对称;
④函数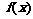 在
在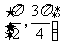 上为减函数;
上为减函数;
其中正确的命题的序号是 ( )
A.②③ B.②④ C.①③ D.①②③
6.一个空间几何体的三视图为全等的等腰直角三角形,若直角三角形的直角边长为1,则这个几何体的体积为( )
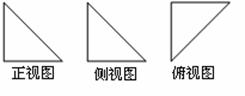
A.1 B.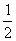 C.
C.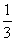 D.
D.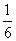
5.设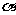 、
、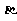 、
、 为平面,a,b为直线,给出下列条件
为平面,a,b为直线,给出下列条件
①a
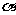 ,b
,b
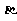 ,a∥
,a∥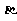 ,b∥
,b∥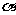 ②
②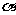 ∥
∥ ,
,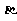 ∥
∥
③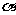 ⊥
⊥ ,
,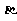 ⊥
⊥ ④a⊥
④a⊥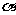 , b⊥
, b⊥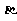 ,a∥b,其中能使
,a∥b,其中能使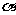 ∥
∥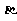 成立的条件有 ( )
成立的条件有 ( )
A.①② B.②③ C.②④ D.③④
4.已知双曲线的离心率为2,焦点是(-4,0),(4,0),则双曲线方程为 ( )
A.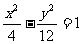 B.
B.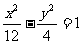
C.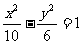 D.
D.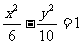
3.已知直线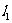 :2x+ay+1=0,
:2x+ay+1=0, 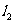 :ax+2y-2=0,若
:ax+2y-2=0,若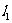 ⊥
⊥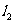 ,则a的值为 ( )
,则a的值为 ( )
A. 0 B. 2 C.任意实数 D.不存在
2.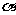 是第四象限角,
是第四象限角,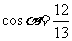 ,sin
,sin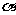 = ( )
= ( )
A.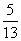 B.-
B.-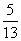 C.
C.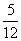 D.-
D.-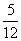
1.设S={x|2x+1>0},T={x|3x-5<0},则S∩T= ( )
A.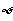 B.{x|x<
B.{x|x<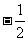 }
}
C.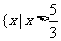 } D.{x|
} D.{x|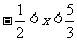 }
}
22.(本小题满分12分)
已知⊙C:x2+(y-1)2=5,直线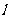 :mx-y+1-m=0
:mx-y+1-m=0
(1)求证:对m∈R,直线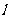 与圆C总有两个不同交点A、B;
与圆C总有两个不同交点A、B;
(2)求弦AB中点M轨迹方程,并说明其轨迹是什么曲线?
(3)若定点P(1,1)分弦AB为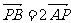 ,求
,求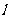 方程。
方程。
21.(本小题满分12分)
已知偶函数f(x),对任意x1,x2∈R,恒有f(x1+x2)=f(x1)+f(x2)+2x1x2+1,求
(1)f(0)的值;
(2)f(x)的表达式;
(3)令F(x)=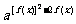 (a>0且a≠1),求F(x)在(0,+∞)上的最值。
(a>0且a≠1),求F(x)在(0,+∞)上的最值。
20.(本小题满分12分)
某商品每件成本9元,售价为30元,每星期卖出432件,如果降低价格,销售量可以增加,且每星期多卖出商品件数与商品单价的降低值x(单位:元,0≤x≤30)的平方成正比,已知商品单价降低2元时,一星期多卖出24件
(1)将一个星期的商品销售利润表示成x的函数;
(2)如何定价才能使一个星期的商品销售利润最大?
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com