
3.若双曲线 的离心率是2,则实数k的值是 ( )
的离心率是2,则实数k的值是 ( )
A.-3 B.-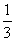 C.3 D.
C.3 D.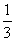
2.函数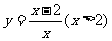 的反函数的定义域为 ( )
的反函数的定义域为 ( )
A. B.
B.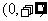 C.(0,1) D.(1,2)
C.(0,1) D.(1,2)
1.在复平面内,复数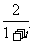 对应的点与原点的距离是 ( )
对应的点与原点的距离是 ( )
A.1 B.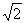 C.2 D.
C.2 D.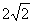
21.(本小题满分14分)已知:三次函数 f(x)=ax3+ bx2+cx + d。
f(x)=ax3+ bx2+cx + d。
(1)如果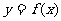 为奇函数,求b,d的值;
为奇函数,求b,d的值;
(2)如果函数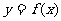 的图象关于其图象上的点(1,2)对称,(-1,-6)为
的图象关于其图象上的点(1,2)对称,(-1,-6)为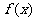 极值点,求此函数在区间[-2,4]上的最值。
极值点,求此函数在区间[-2,4]上的最值。
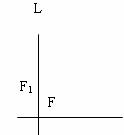
20.(本小题满分14分)如图,定点F到定直线L的距离(线段FF1)为p,⊙P过F且和L相切,
(1)求圆心P的轨迹S;
(2)过F作轨迹S的两条弦AB、CD(A、C在直线FF1的同侧),求证:直线AC和BD的交点在直线L上。
19.(本小题满分14分)如图所示的几何体由斜三棱柱ABC-A1B1C1和A2B2C2-A1B1C1组成,其斜三棱ABC-A1B1C1和斜三棱柱A2B2C2-A1B1C1满足 ABB1A1≌
ABB1A1≌  A2B2B1A1 ,
A2B2B1A1 , BCC1B1≌
BCC1B1≌  B2C2C1B1,
B2C2C1B1, CAA1C1≌
CAA1C1≌ C2A2A1C1
C2A2A1C1
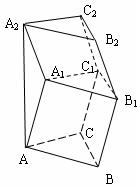
(1)证明AA2⊥A1C1
(2)证明AA2⊥面ABC
(3)若AB=AC=AA1,∠CAB=90°,面AA1B⊥面ABC,问:侧棱AA1和底面ABC所成的角是多少度时,A1C2∥面BCC1B1
18.(本小题满分13分)已知: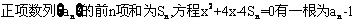
(1)求数列
(2)
17.(本小题满分12分)某交通环岛有三岔路口,有6辆汽车汇入环岛内,都等可能地从其中一个路口驶出环岛。
(1)求按1,2,3的数量从三岔路口驶出环岛的情况有多少种?
(2)如果从三岔路口中某一路口恰好驶出n辆车的概率为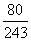 ,求n的值。
,求n的值。
16.(本小题满分12分)已知:m = (cos ,1 + sin
,1 + sin ), n = (1+cos
), n = (1+cos , sin
, sin )
)
(1)如果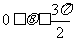 ,m·n =
,m·n = ,求tan
,求tan -cot
-cot
(2)如果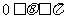 求
求 的取值范围
的取值范围
15.已知函数f(x),g(x)分别由下表给出定义:
|
x |
1 |
2 |
3 |
|
f(x) |
2 |
|
3 |
|
x |
1 |
2 |
3 |
|
g(x) |
3 |
3 |
1 |
若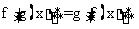 的解恰有2个,请在表中空白的部分填上合适的一组数。(只要写出一组数,不必写出全部解)
的解恰有2个,请在表中空白的部分填上合适的一组数。(只要写出一组数,不必写出全部解)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com