
17.(本小题满分12分)
设一袋中装有白球和黑球,已知两种球的数目之比为1:3,但不知哪种球较多,因而从袋中任取一球得黑球的概率P是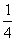 或
或 ,现从中有放回地任取三个球,试以此来估计P究竟是
,现从中有放回地任取三个球,试以此来估计P究竟是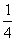 还是
还是 .试述你估计的理由.
.试述你估计的理由.
16.(本小题满分12分)
在 ABC中,
ABC中, ,△ABC的面积为S.
,△ABC的面积为S.
(1)求∠A的值;
(2)证明: .
.
15.用砖砌墙,第一层(底层)用去全部砖块的一半多一块,第二层用去剩下的一半多一块,……依次类推,每一层都用去了上一层剩下的砖块的一半多一块,如果到第九层恰好用完砖块,那么一共用了___________块砖.
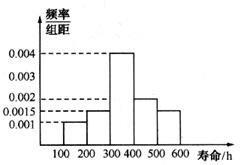
14.某厂研究生产了一种新型电子元件,现随机从中抽取了200个元件进行寿命终极度试验,得到频率分布直方图如图.则寿命在100-200h的元件有________个;估计合格品(寿命在100-400h)的概率为__________;估计总体寿命平均值为__________.
13.正三角形的三个顶点在双曲线 的右支上,其中一个顶点与双曲线右顶点重合,则
的右支上,其中一个顶点与双曲线右顶点重合,则 的取值范围是____________.
的取值范围是____________.
12.设二项式(1+2 )n的展开式中的各项系数和为
)n的展开式中的各项系数和为 ,二项式系数和为bn,且
,二项式系数和为bn,且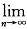 =
= ,则
,则 的值等于_____________.
的值等于_____________.
11.定义非空集合A的真子集的真子集是A的“孙集”,则集合{1,3,5,7,9}的“孙集”的个数为_____________个.
10.已知椭圆的离心率为 ,两焦点分别为F1,F2,抛物线C以F1为顶点、F2为焦点,点P为抛物线和椭圆的一个交点,若
,两焦点分别为F1,F2,抛物线C以F1为顶点、F2为焦点,点P为抛物线和椭圆的一个交点,若 |PF2|=|PFl|,则
|PF2|=|PFl|,则 的值为
的值为
A.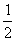 B.
B. C.
C. D.以上均不对
D.以上均不对
第Ⅱ卷(非选择题 共100分)
9.如图所示,在单位正方体ABCD-A1B1C1D1的面对角线A1B1存在一点P,使AP+D1P取得最小值,则此最小值为
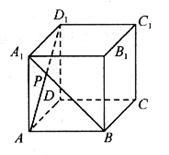
A.2
B. B.
B. D.
D.
8.若 R,
R, ,定义:
,定义: ,如
,如 ,则函数
,则函数
A.是偶函数不是奇函数 B.是奇函数不是偶函数
C.既是奇函数又是偶函数 D.既不是奇函数也不是偶函数
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com