
6.已知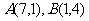 ,直线
,直线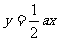 与线段AB交于点C,且
与线段AB交于点C,且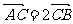 ,则
,则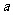 等于
等于
A. B.
B.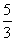 C.
C.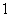 D.
D.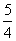
5.当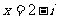 时,
时, 等于
等于
A.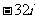 B.32 C.
B.32 C.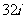 D.
D.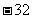
4.设正三棱锥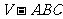 的底边长为
的底边长为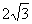 ,高为2,则侧棱与底面所成角的大小为
,高为2,则侧棱与底面所成角的大小为
A.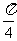 B.
B.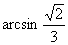 C.
C.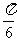 D.
D.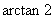
3.函数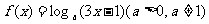 的反函数的图像过定点
的反函数的图像过定点
A.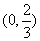 B.
B.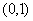
C.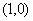 D.
D.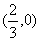
2.已知函数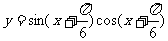 ,则其最小正周期和图像的一条对称轴方程分别为
,则其最小正周期和图像的一条对称轴方程分别为
A.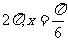 B.
B.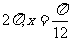
C.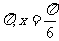 D.
D.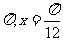
1.已知集合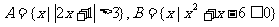 ,则
,则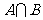 等于
等于
A.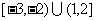 B.
B.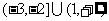
C.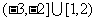 D.
D.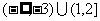
21.(本小题满分14分)
已知函数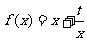 (
(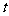 >0),过点P(1,0)作曲线
>0),过点P(1,0)作曲线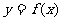 的两条切线PM、PN,为M、N.
的两条切线PM、PN,为M、N.
(1)当t=2时,求函数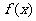 的单调递增区间;
的单调递增区间;
(2)设|MN|=g(t),求函数g(t)的表达式;
(3)在(2)的条件下,若对任意正整数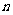 ,在区间[2,
,在区间[2,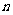 +
+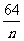 ]内总存在
]内总存在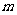 +1个实数
+1个实数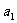 、
、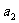 、…、
、…、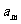 、
、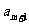 ,使得不等式g(
,使得不等式g(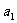 )+g(
)+g(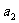 )+…+g(
)+…+g(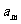 )<g(
)<g(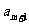 )成立,求
)成立,求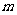 的最大值.
的最大值.
20.(本小题满分13分)
如图所示的一组图形为某一四棱锥S-ABCD的侧面与底面;
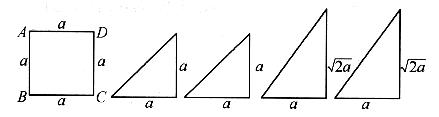
(1)请画出四棱锥S-ABCD的示意图,并判断是否存在一条侧棱垂直于底面?如果存在,请给出证明;
(2)若SA⊥平面ABCD,E为AB中点,求二面角E-SC-D的大小;
(3)在(2)的条件下,求点D到平面SEC的距离.
19.(本小题满分12分)
已知椭圆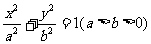 的一条准线方程是
的一条准线方程是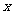 =1,过椭圆的左焦点F,且方向向量为
=1,过椭圆的左焦点F,且方向向量为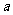 =(1,1)的直线
=(1,1)的直线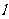 交椭圆于A、B两点,AB的中点为M.
交椭圆于A、B两点,AB的中点为M.
(1)求直线OM的斜率(用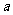 、b表示):
、b表示):
(2)直线AB与OM的夹角为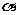 ,当tan
,当tan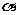 =2时,求椭圆的方程;
=2时,求椭圆的方程;
(3)当A、B两点位于第一、三象限时,求椭圆短轴长的取值范围.
18.(本小题满分12分)
某县农民平均收入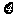 服从正态分布,其中
服从正态分布,其中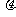 =500,
=500,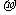 =20.
=20.
(1)求此县农民年均收入在500~520元之间的人数的百分比;
(2)若要使农民的年均收入在(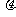 -
-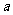 ,
,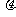 +
+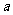 )内的概率不小于0.95,则
)内的概率不小于0.95,则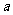 的值应至少为多大?
的值应至少为多大?
[备选数据: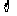 (0)=0.5000,
(0)=0.5000,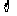 (1)=0.8413,
(1)=0.8413,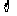 (1.96)=0.9750]
(1.96)=0.9750]
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com