
4.在R上定义一种运算 :x
:x y=x(1–y).若不等式(x–a)
y=x(1–y).若不等式(x–a) (x+a)<1对任意实数x成立,则 ( )
(x+a)<1对任意实数x成立,则 ( )
A.–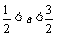 B.0<a<2 C.–1<a<1 D.
B.0<a<2 C.–1<a<1 D.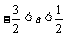
3.已知定义在R上的函数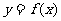 满足以下三个条件:①对于任意的
满足以下三个条件:①对于任意的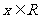 ,都有
,都有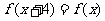 ;②对于任意的
;②对于任意的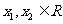 ,且
,且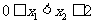 ,都有
,都有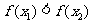 ;③函数
;③函数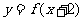 的图象关于
的图象关于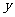 轴对称,则下列结论中正确的是 ( )
轴对称,则下列结论中正确的是 ( )
A.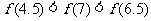 B.
B.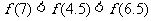
C.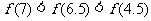 D.
D.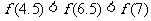
2.已知函数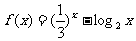 ,
,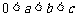 ,
,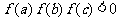 ,实数
,实数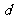 是函数
是函数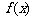 的一个零点.给出下列四个判断:①
的一个零点.给出下列四个判断:①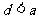 ;②
;②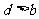 ;③
;③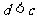 ;④
;④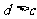 .其中可能成立的个数为 ( )
.其中可能成立的个数为 ( )
A.1 B.2 C.3 D.4
1.已知下表中的对数值有且只有一个是错误的.
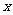 |
1.5 |
3 |
5 |
6 |
8 |
9 |
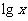 |
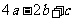 |
 |
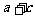 |
 |
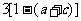 |
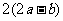 |
其中错误的对数值是 ( )
A.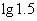 B.
B.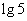 C.
C.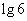 D.
D.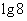
22.(本小题满分12分)
已知定义在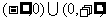 上的函数
上的函数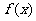 满足
满足
①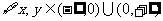 ,
,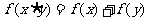 ;
;
②当 时,
时,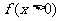 ,且
,且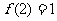 。
。
(1)试判断函数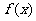 的奇偶性;
的奇偶性;
(2)判断函数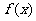 在(0,+∞)上的单调性;
在(0,+∞)上的单调性;
(3)求函数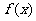 在区间
在区间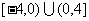 上的最大值;
上的最大值;
(4)求不等式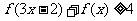 的解集。
的解集。
21.(本小题满分10分)
已知函数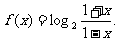
(1)判断函数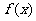 的奇偶性;
的奇偶性;
(2)求证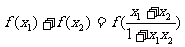
(3)若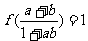 ,
, ,求
,求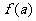 的值。
的值。
20.(本小题满分10分)
已知奇函数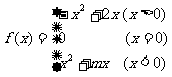 。
。
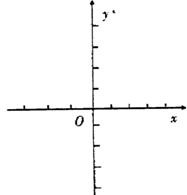
(1)求实数m的值,并在给出的直角坐标系中画出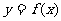 的图象;
的图象;
(2)若函数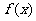 在区间
在区间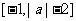 上单调递增,试确定
上单调递增,试确定 的取值范围。
的取值范围。
19.(本小题满分10分)
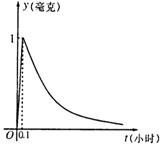
为了预防甲型H1N1流感,某学校对教室用某种药物进行消毒。已知药物释放过程中,室内每立方米空气中的含药量y(毫克)与时间t(小时)成正比;药物释放完毕后,y与t的函数关系式为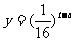 (
( 为常数),如图所示,根据图中提供的信息,回答下列问题:
为常数),如图所示,根据图中提供的信息,回答下列问题:
(1)求从药物释放开始,每立方米空气中的含药量y(毫克)与时间t(小时)之间的函数关系式。
(2)据测定,当空气中每立方米的含药量降低到0.25毫克以下时,学生方可进教室,那么从药物释放开始,至少需要经过多少小时后,学生才能回答教室。
18.(本小题8分)
已知 ,且
,且 ≠1,设
≠1,设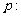 函数
函数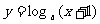 在
在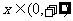 内单调递减;q:函数
内单调递减;q:函数
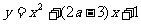 有两个不同零点点,如果
有两个不同零点点,如果 和
和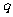 有且只有一个正确,求
有且只有一个正确,求 的取值范围。
的取值范围。
17.(本小题6分)计算
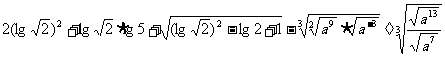
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com