
22.(本小题满分14分)已知数列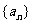 ,
,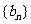 中,
中,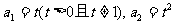 ,且
,且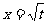
是函数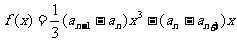 的一个极值点.
的一个极值点.
(I)求数列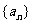 的通项公式;
的通项公式;
(II)已知点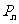 的坐标为
的坐标为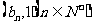 ,若直线
,若直线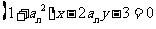 始终与
始终与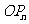 平行(
平行(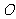 为原点),求证:当
为原点),求证:当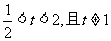 时,不等式
时,不等式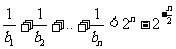 对任意
对任意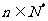 都成立.
都成立.
21.(本小题满分12分)已知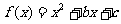 为偶函数,曲线
为偶函数,曲线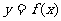 过点
过点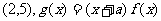 .
.
(I)若曲线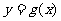 有斜率为
有斜率为 的切线,求实数
的切线,求实数 的取值范围;
的取值范围;
(II)若当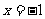 时,函数
时,函数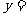
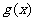 取得极值,且方程
取得极值,且方程 有三个不同的实数解,求实数
有三个不同的实数解,求实数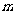 的取值范围.
的取值范围.
20.(本小题满分12分)设数列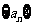 的前
的前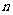 项和为
项和为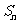 ,且满足
,且满足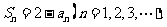
(I)求数列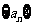 的通项公式;
的通项公式;
(II)若数列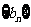 满足
满足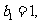 且
且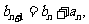 求数列
求数列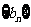 的通项公式;
的通项公式;
(III)设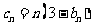 ,求数列
,求数列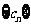 的前
的前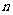 项和
项和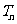 .
.
19.(本小题满分12分)已知函数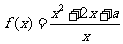 .
.
(I)若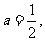 当
当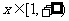 时,求
时,求 的最小值;
的最小值;
(II)当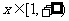 时,
时,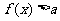 恒成立,试求实数
恒成立,试求实数 的取值范围.
的取值范围.
18.(本小题满分12分)加工某种零件需经过三道工序,设第一、二、三道工序的合格率分别为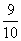 、
、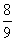 、
、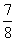 ,且各道工序互不影响.
,且各道工序互不影响.
(I)求该种零件的合格率;
(II)从该种零件中任取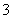 件,求恰好取到一件合格品的概率;
件,求恰好取到一件合格品的概率;
(III)从该种零件中任取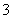 件,求至少取到一件合格品的概率.
件,求至少取到一件合格品的概率.
17.(本小题满分12分)在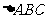 中,角
中,角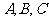 的对边分别为
的对边分别为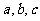 ,且满足
,且满足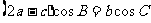 .
.
(I)求角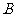 的大小;
的大小;
(II)设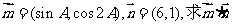 的最大值.
的最大值.
16.①若 是定义在
是定义在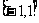 上的偶函数,且在
上的偶函数,且在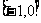 上是增函数,
上是增函数,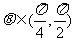 ,则
,则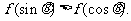
②在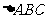 中,
中,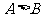 是
是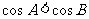 的充要条件.
的充要条件.
③若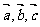 为非零向量,且
为非零向量,且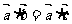 ,则
,则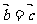 .
.
④要得到函数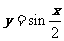 的图像,只需将函数
的图像,只需将函数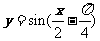 的图像向右平移
的图像向右平移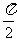 个单位.
个单位.
⑤函数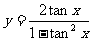 是奇函数.
是奇函数.
其中真命题的有__________.
15.若不等式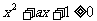 对一切
对一切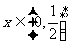 成立,则
成立,则 的最小值为
.
的最小值为
.
14.在数列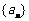 中,
中,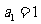 ,
,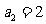 且
且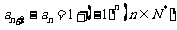 ,则
,则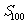 =
.
=
.
13.已知函数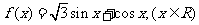 )的一条对称轴为直线
)的一条对称轴为直线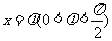 ,则
,则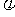 的值为
.
的值为
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com