
20.已知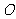 为坐标原点,点
为坐标原点,点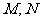 分别在
分别在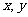 轴上运动,且
轴上运动,且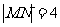 ,动点
,动点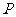 满足
满足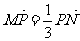 .
.
(I)求动点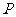 的轨迹
的轨迹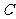 的方程.
的方程.
(II)过点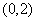 的直线
的直线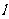 与
与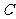 交于不同两点
交于不同两点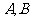 .
.
①求直线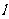 斜率
斜率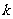 的取值范围. ②若
的取值范围. ②若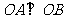 ,求直线
,求直线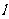 的方程.
的方程.
19.正项数列 ,其前
,其前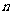 项和为
项和为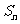 并且满足:
并且满足: 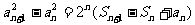 且
且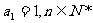 .
.
(I)求数列 的通项公式.
的通项公式.
(II)若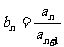 ,判断数列
,判断数列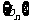 的单调性,并证明之.
的单调性,并证明之.
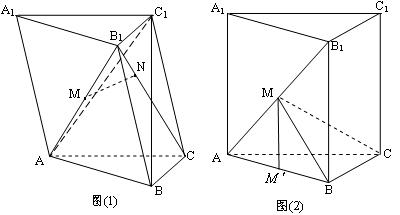
18.三棱柱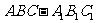 .
.
(I)如图(1)若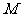 是
是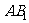 的中点, 点
的中点, 点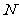 在
在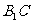 上,且
上,且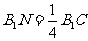 ,证明:
,证明: 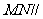 平面
平面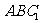
(II)如图(2)若点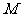 在
在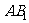 上,且在平面
上,且在平面 上的正射影为
上的正射影为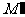 ,且
,且 ,又
,又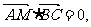
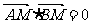 .求二面角
.求二面角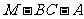 的平面角的大小.
的平面角的大小.
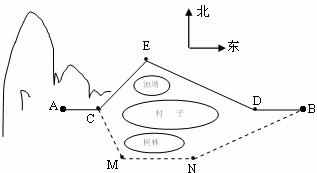
17.某村子的正西是一片山区。山脚下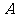 处已建一处采石场,村子的北边有一池塘,南边有一树林,在
处已建一处采石场,村子的北边有一池塘,南边有一树林,在 处是个石粉厂,在采石场采到的石料由公路
处是个石粉厂,在采石场采到的石料由公路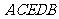 运输到石粉厂,如图所示.已知
运输到石粉厂,如图所示.已知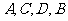 在一条直线上,
在一条直线上,
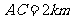 ,
,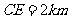 ,
,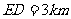 ,
, ,
, .
.
(I)求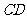 的长.
的长.
(II)在运作了一段时间后,发现在运输车经过公路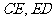 时对池塘有污染,需要另建公路
时对池塘有污染,需要另建公路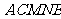 。为了不破坏树林,必须要求
。为了不破坏树林,必须要求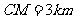 ,
,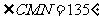 ,
,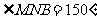
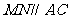 。求建这条新的公路中
。求建这条新的公路中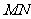 的长.
的长.
16.已知抛物线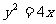 ,焦点
,焦点 ,在其准线上有两点
,在其准线上有两点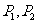 ,在此抛物线上有两点
,在此抛物线上有两点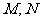 ,使得
,使得 为以
为以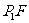 为斜边的等腰直角三角形,
为斜边的等腰直角三角形, 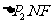 为正三角形,则线段
为正三角形,则线段 的最小值为
.
的最小值为
.
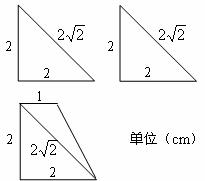
15.某几何体的三视图如右图,则此几何体的体积为 .
14.已知数列 是等比数列,且
是等比数列,且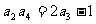 ,则
,则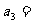 .
.
13.若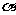 是第三象限角,且
是第三象限角,且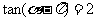 ,则
,则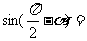 .
.
12.方程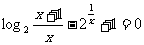 实根的个数是:(
)
实根的个数是:(
)
A. 个
B.
个
B.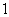 个
C.
个
C. 个 D.
个 D.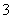 个
个
第II卷(非选择题,满分90分)
11.定义在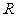 上的奇函数
上的奇函数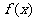 满足:①在
满足:①在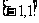 上的解析式为
上的解析式为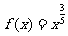 ;②函数
;②函数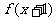 是偶函数,则
是偶函数,则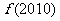 的值是:( )
的值是:( )
A. B.
B.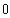 C.
C.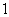 D.
D.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com