
18.(本小题满分12分)
某学生在上学路上要经过4个路口,假设在各路口是否遇到红灯是相互独立的,遇到红灯的概率都是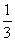 ,遇到红灯时停留的时间都是2min。
,遇到红灯时停留的时间都是2min。
(1)求这名学生在上学路上到第三个路口时首次遇到 红灯的概率;
(2)求这名学生在途中至少遇到一次红灯的概率;
(3)求这名学生在上学路上因遇到红灯停留的总时间ξ的分布列及期望。
17.(本小题满分12分)
已知函数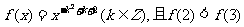 。
。
(1)求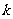 的值;
的值;
(2)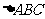 中,
中,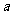 、
、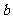 、
、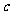 分别是角
分别是角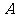 、
、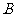 、
、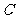 的对边,已知
的对边,已知
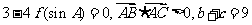 ,
,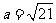 ,求
,求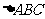 的面积。
的面积。
16.(本小题满分12分)
已知数列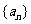 的前
的前 项和为
项和为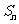 ,数列
,数列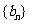 的前
的前 项和为
项和为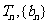 为等差数列且各项均为正数,
为等差数列且各项均为正数,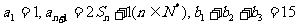
(1)求数列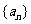 的通项公式;
的通项公式;
(2)若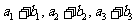 成等比数列,求
成等比数列,求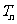
15.已知函数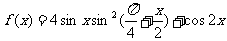
(I)设 为常数,若
为常数,若 上是增函数,则
上是增函数,则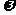 的取值范围是_____________。
的取值范围是_____________。
(II)若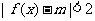 成立的充分条件是
成立的充分条件是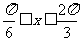 ,则实数m的取值范围是________。
,则实数m的取值范围是________。
14.若某一等差数列的首项为 ,公差为
,公差为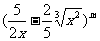
展开式的常数项,其中m是7777-15除以19的余数 ,则此数列的前_________项和最大,最大值为_________。
,则此数列的前_________项和最大,最大值为_________。
13.在计算“1×2+2×3+…n(n+1)”时,某同学学到了如下一种方法:
先改写第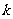 项:
项: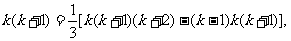
由此得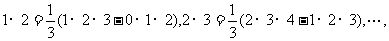
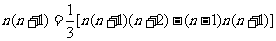
相加,得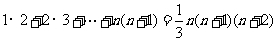
类比上述方法,请你 计算“
计算“ ”,其,结果为______。
”,其,结果为______。
12.如果直线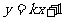 与圆
与圆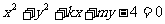 相交于M、N两点,
相交于M、N两点, 且点M、N关于直线
且点M、N关于直线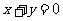 对称,则不等式组
对称,则不等式组 所表示的平面区域的面积为_________。
所表示的平面区域的面积为_________。
11.三点(3,10),)(7,20),(11,24)的回归方程是_________。
10.在下图中,从上往下连接“构建和谐社会,创美好未来”(不能跳跃),共有________种不同的连法。(用数字作答)

9.不等式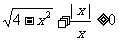 的解集为___________________。
的解集为___________________。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com