
4. 判断下列命题的真假:
⑴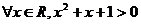 ;
⑵
;
⑵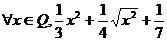 是有理数;
是有理数;
⑶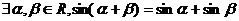 ; ⑷
; ⑷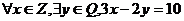 ;
;
⑸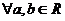 ,方程
,方程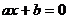 恰有一实数解.
恰有一实数解.
[典型例题]
例1. 在下列结论中,①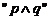 为真是
为真是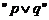 为真的充分不必要条件;
为真的充分不必要条件;
②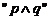 为假是
为假是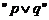 为真的充分不必要条件;
为真的充分不必要条件;
③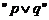 为真是
为真是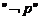 为假的必要不充分条件;
为假的必要不充分条件;
④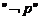 为真是
为真是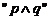 为假的必要不充分条件;
为假的必要不充分条件;
正确的是________ _______.
练习:由下列各组命题构成的“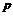 或
或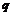 ”、“
”、“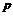 且
且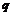 ”“非
”“非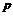 ”形式的命题中,“
”形式的命题中,“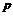 或
或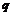 ”为真,“
”为真,“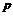 且
且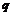 ”为假,“非
”为假,“非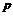 ”为真的是
( )
”为真的是
( )
A.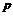 :3是偶数,
:3是偶数,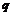 :4是奇数; B
:4是奇数; B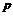 :3+2=6,
:3+2=6, 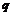 :5>3;
:5>3;
C.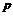 :
: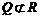 ,
, 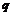 :
: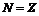 ; D
; D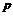 :菱形对角线互相平分,
:菱形对角线互相平分,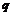 :菱形对角线互相垂直
:菱形对角线互相垂直
例2.写出下列命题的否定并判别真假。
(1) 全等的三角形是相似三角形。
(2) 若x,y都是奇数,则x+y是偶数。
(3) 若xy=0,则x=0或y=0。
(4) 至少有一个实数x,使得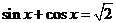
练习:对于下述命题p,写出“非p”形式的命题,并判断“p”与“非p“的真假:
⑴p:91∈A∩B(其中全集U=N*,A={质数},B={正奇数}).
⑵p:底面是正多边形的棱锥是正棱锥.
⑶p:任意正整数都是质数或合数.
⑷p:三角形有且仅有一个外接圆.
[课堂检测]
3. 命题p:存在实数m,使方程x2+mx+1=0有实数根,则“非p”形式的命题是 __ _______________.
2.写出命题“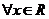 ,
, 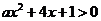 ”的否定形式
.
”的否定形式
.
1.指出命题“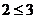 ”的形式是 ,
判定它的真假为 。写出该命题的否定为
.
”的形式是 ,
判定它的真假为 。写出该命题的否定为
.
3.命题的否定与否命题的区别,全称性命题的否定为存在性命题,存在性命题的否定为全称性命题.
[基础训练]
2.复合命题形式的真假判别方法;
|
p |
q |
非p |
P或q |
P且q |
|
真 |
真 |
|
|
|
|
真 |
假 |
|
|
|
|
假 |
真 |
|
|
|
|
假 |
假 |
|
|
|
1.常见词语的否定:如:“等于、大于、小于、是、都是、至多一个、至少一个、任意的、所有的、至多n个、任意两个、或、且”的否定分别是:
2.
设有两个命题:(1)关于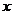 的不等式
的不等式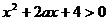 对一切
对一切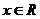 恒成立;(2)函数
恒成立;(2)函数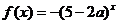 是减函数,若命题有且只有一个是真命题,求实数
是减函数,若命题有且只有一个是真命题,求实数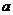 的取值范围。
的取值范围。
1.已知函数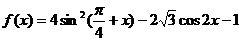 ,条件
,条件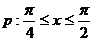 ,条件
,条件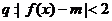 ,若p是q的充分条件,求实数m的取值范围。
,若p是q的充分条件,求实数m的取值范围。
2. 判断命题“若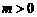 ,则
,则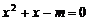 有实数根”的逆否命题的真假;
有实数根”的逆否命题的真假;
[课堂作业]
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com