
6. 常见的结论:
⑴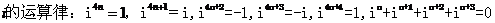 ;
;
⑵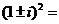 ;
;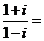 ;
;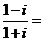 ;
;
⑶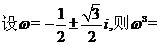 ;
;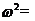 ;
;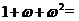 ;
;
[基本训练]
5.复数的模:向量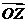 的模叫做复数
的模叫做复数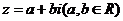 的 (或 ),
的 (或 ),
记作 (或 ),即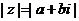 =
;
=
;
复数模的性质:⑴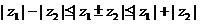 ;⑵
;⑵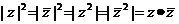 ;
;
4.复平面的概念:建立直角坐标系来表示复数的平面叫做 , 叫做实
轴, 叫做虚轴;实轴上的点表示 ,除原点外,虚轴上的点都表示 .
3.复数的加、减、乘、除去处法则:设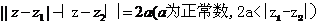 则
则
⑴加法: 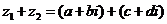 =
;
=
;
⑵减法: 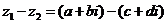 =
;
=
;
⑶乘法: 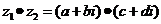 =
;
=
;
⑷乘方: 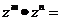 ;
;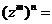 ;
;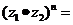 ;
;
⑸除法: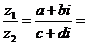
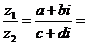 =
;
=
;
2.复数的概念及分类:⑴概念:形如 的数叫做 ,其中
的数叫做 ,其中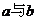 分别为它的 和
.
分别为它的 和
.
⑵分类:①若 为实数,则
,②若
为实数,则
,②若 为虚数,则
,③若
为虚数,则
,③若 为纯虚数,则 ;
为纯虚数,则 ;
⑶复数相等:若复数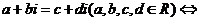 ;
;
⑷共轭复数: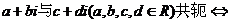 ;
;
1.数的扩展:数系扩展的脉络是:
→ →
,用集合符号表示为 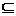
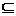 ,实际上前者是后者的真子集.
,实际上前者是后者的真子集.
4.设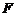 为抛物线
为抛物线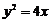 的焦点,
的焦点,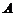 、
、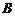 、
、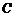 为该抛物线上三点,若
为该抛物线上三点,若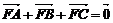 ,则
,则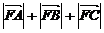 =___________.
=___________.
3.抛物线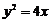 的焦点为
的焦点为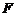 ,准线为
,准线为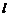 ,经过
,经过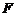 且斜率为
且斜率为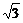 的直线与抛物线在
的直线与抛物线在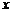 轴上方的部分相交于点
轴上方的部分相交于点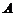 ,
,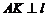 ,垂足为
,垂足为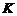 ,则
,则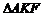 的面积是__________.
的面积是__________.
2.连接抛物线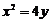 的焦点
的焦点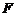 与点
与点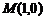 所得的线段与抛物线交于点
所得的线段与抛物线交于点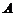 ,设点
,设点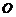 为坐标原点,则三角形
为坐标原点,则三角形 的面积为__________.
的面积为__________.
1.已知点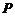 为抛物线
为抛物线 上的动点,点
上的动点,点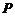 在
在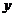 轴上的射影是
轴上的射影是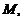 点
点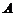 的坐标是
的坐标是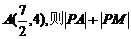 的最小值是
的最小值是
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com