
3.若直线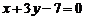 和
和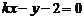 与
与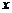 轴、
轴、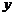 轴正方向所围成的四边形有外接圆,则
轴正方向所围成的四边形有外接圆,则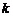 为________________.
为________________.
[典型例题]
例1 已知两直线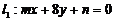 和
和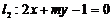 ,试确定
,试确定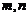 的值,使
的值,使
(1)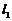 与
与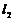 相交于点
相交于点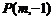 ;(2)
;(2)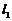 ∥
∥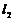 ;(3)
;(3)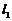 ⊥
⊥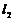 ,且
,且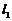 在
在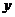 轴上的截距为
轴上的截距为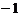 .
.
变式 “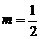 ” 是“直线
” 是“直线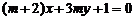 与另外一条直线
与另外一条直线
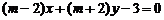 相互垂直”的_______________________条件.
相互垂直”的_______________________条件.
例2已知直线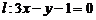 ,在
,在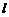 上求一点
上求一点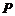 ,使得:
,使得:
(1) 到点
到点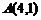 和
和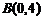 的距离之差最大;(2)
的距离之差最大;(2) 到点
到点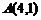 和
和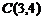 的距离之和最小.
的距离之和最小.
变式. 过点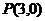 作直线
作直线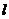 ,使它被相交直线
,使它被相交直线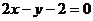 和
和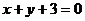 所截得的线段恰好被
所截得的线段恰好被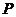 点平分,求直线
点平分,求直线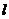 的方程.
的方程.
[课堂小结]1.两条直线平行与垂直的判断;2.两条直线的到角与夹角.
[课堂检测]
2.过坐标原点且与点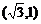 的距离都等于1的两条直线的夹角为
的距离都等于1的两条直线的夹角为
1.直线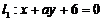 与直线
与直线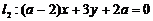 ,当
,当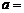 ___________时,
___________时,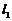 ∥
∥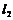 ;当
;当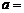 ___________时,
___________时,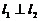 ;当
;当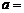 ___________时,
___________时,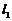 与
与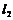 相交;当
相交;当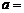 _________时,
_________时,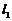 与
与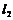 重合.
重合.
2.已知过点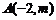 和
和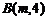 的直线
的直线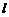 与已知直线
与已知直线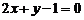 平行,则实数
平行,则实数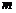 的值为__________________.
的值为__________________.
[基本训练]
1.两直线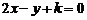 和
和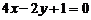 的位置关系是_________________.
的位置关系是_________________.
2.两直线的交点坐标之间的关系,体会数形结合的思想。
[基础知识]
1.两直线的平行与垂直,两点间的距离公式,点到直线的距离公式及简单应用,平行线间的距离;
5.定义在(-1,1)上的函数f(x)是奇函数,并且在(-1,1)上f(x)是减函数,求满足条件f(1-a)+f(1-a2)<0的a取值范围.
4.函数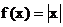 和
和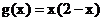 的递增区间依次是
的递增区间依次是
3.若函数是奇函数,当x<0时,f(x)的解析式是f(x)=x(1-x),则当x>0时,f(x)的解析式是 .
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com