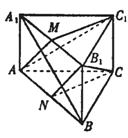
3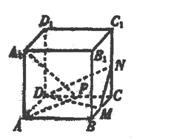．如图，M，N，P分别是正方体ABCD-A₁B₁C₁D₁的棱BC，CC₁，CD的中点，求证：平面A₁AP⊥平面MND.

2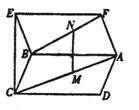．如图，ABCD，ABEF均为平行四边形，M，N

分别为对角线AC，FB上的点，且有，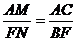

求证：MN∥平面CBE.

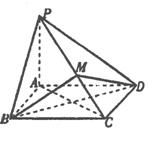
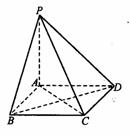
1．如图，在四棱锥P-ABCD中，PA⊥底面ABCD．

底面各边都相等，M是PC上的一动点，当点M满足

_______________________时，平面MBD⊥平面PCD.

5．设平面α∥β，A、C∈α，B、D∈β，直线AB与CD

交于S，若AS = 18，BS = 9，CD = 34，则CS = _____________.

§98平面与平面的位置关系(2)

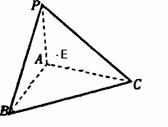
例3．已知：如图，平面PAB⊥平面ABC，平面PAC⊥平面ABC，E是点A在平面PBC内的射影.

(1)求证：PA⊥平面ABC；(2)当E为△PBC的垂心时，求证：△ABC是直角三角形.

例4．直三棱柱ABC-A₁B₁C₁中，B₁C₁ = A₁C₁，AC₁⊥A₁B，M，N分别是A₁B₁，AB的中点(如图). (1)求证：C₁M⊥平面A₁ABB₁；(2)求证：A₁B⊥AM；

(3)求证：平面AMC₁∥平面NB₁C.

[课后作业]

4．如图，已知四边形ABCD是正方形，PA⊥平面ABCD，

则图中所有互相垂直的平面共有 　　　　　　　　　　　　　 (　　 )

A．8对

B．7对

C．6对

D．5对

3．设α，β为两个不同的平面，，m为两条不同的直线，且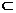α，m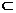β，有如下的两个命题：①若α∥β，则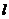∥m；②若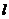⊥m，则α⊥β. 那么　　 (　)　　　　　　　　　　 A　 ①是真命题，②是假命题　　　　　　　　　 B　 ①是假命题，②是真命题

C　 ①②都是真命题　　　　　　　　　　　　　　　　 D　 ①②都是假命题　　

2．平面α⊥平面β，α∩β= ，点P∈α，点Q∈，那么PQ⊥是PQ⊥β的(　　 )

A　 充分但不必要条件　　　　　　　　　　　　　　 B　 必要但不充分条件

C　 充要条件　　　　　　　　　　　　　　　　　　　　　 D　 既不充分也不必要条件

1．若α，β表示平面，a，b表示直线，则a∥α的一个充分条件是(　　 )　　　　　　　　 A　 α⊥β，且a⊥β　　　　　 　　　　　　　　　　 B　 α∩β= b，且a∥b

C　 a∥b，且b∥α　　　　　　　　　　　　　　　　　 D　 α∥β，且a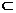β

6．如图，直线AC，DF被三个平面α，β，γ所截，若AC

与α成30°角，AB = 4，BC = 12，DF = 10，则平面β，γ间距

离为__________，DE = __________，EF = _________.

[典型例题讲练]

例1．已知：平面α∥平面β，AB，CD是异面直线，

A∈α，C∈α，B∈β，D∈β，E，F分别为AB，CD的

中点，求证：EF∥α∥β.

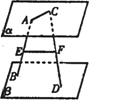
例2．如图，△ABC为正三角形，EC⊥平面ABC，BD∥CE，且CE = CA = 2BD，M是EA中点. 求证：(1)DE = DA；(2)平面MBD⊥平面ECA；(3)平面DEA⊥平面ECA.

[课堂小结]

[课堂检测]

5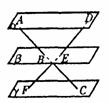．在正四面体P-ABC中，D，E，F分别是AB，BC，CA的中点，下面四个结论中，不成立的是　　　 (　　 )　　　 　　　　　　　　　　　　　　　　　　　　　 　　　　　　　　　　　　　　　　　　　　　　　　　　　　 A　 BC∥平面PDF　　　　　　　　　　 B　 DF⊥平面PAE

C　 平面PDF⊥平面ABC　　　　　 D　 平面PAE⊥平面ABC