
2.已知点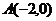 、
、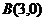 ,动点
,动点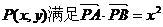 ,则点P的轨迹是( )
,则点P的轨迹是( )
A. 圆 B. 椭圆 C. 双曲线 D. 抛物线
1.设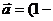 cos
cos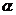 ,
,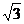 ),
), 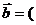 sin
sin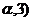 ,且
,且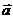 ∥
∥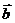 , 则锐角
, 则锐角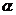 为
为
8.已知a2=2a·b,b2=2a·b,则a与b的夹角为
A.0° B.30° C.60° D.180°
§44 平面向量 4 (2)
[典型例题讲练]
例3圆O内两弦AB、CD垂直相交于P点,求证: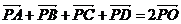 .
.
变式: 已知△ABC中,A(2,-1),B(3,2),C(-3,-1),BC边上的高为AD,求点D和向量AD的坐标.
例4.已知A(3,0),B(0,3),C(cos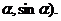
(1)若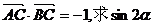 的值;
的值;
(2)若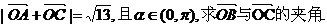
变式1: 平面直角坐标系中,O为坐标原点, 已知两点A(3, 1), B(-1, 3),若点C满足
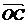 =
=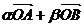 , 其中α、β∈R且α+β=1, 则点C的轨迹方程为
, 其中α、β∈R且α+β=1, 则点C的轨迹方程为
变式2: 已知空间四边形ABCD的每条边和对角线的长都等于m,点E,F分别是BC,AD的中点,则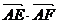 的值为
的值为
[课堂小结]
针对向量坐标表示的应用,通过非坐标形式解法与坐标化解法的比较来加深学生对于向量坐标表示的认识,同时要加强学生选择建立坐标系的意识.在综合学习向量知识之后,解决问题的途径较多,可以考虑两向量垂直的充要条件的应用,也可考虑平面图形的几何性质.
[课堂检测]
7.已知向量i,j,i=(1,0),j=(0,1)与2i+j垂直的向量为
A.2i-j B.i-2j C.2i+j D.i+2j
6.若i=(1,0),j=(0,1),则与2 i+3j垂直的向量是
A.3i+2j B.-2i+3j C.-3i+2j D.2i-3j
5.设a=(-1,2),b=(1,-1),c=(3,-2)且c=pa+qb,则实数p、q的值为
A.p=4,q=1 B.p=1,q=4 C.p=0,q=1 D.p=1,q=-4
4.若|a|=|b|=1,a⊥b,且2a+3b与ka-4b也互相垂直,则k的值为
A.-6 B.6 C.3 D.-3
3.已知|a|=3,|b|=4,(a+b)·(a+3b)=33,则a与b的夹角为
A.30° B.60° C.120° D.150°
1.熟悉向量的性质及运算律;2.能根据向量性质特点构造向量;3.熟练平面几何性质在解题中应用;4.熟练向量求解的坐标化思路.
[课堂检测]
1当|a|=|b|≠0且a、b不共线时,a+b与a-b的关系是
A.平行 B.垂直
C.相交但不垂直 D.相等
2下面有五个命题,其中正确的命题序号为
①单位向量都相等;②长度不等且方向相反的两个向量不一定是共线向量;③若a,b满足|a|>|b|且a与b同向,则a>b;④由于零向量方向不确定,故0不能与任何向量平行;⑤对于任意向量a,b,必有|a+b|≤|a|+| b |
A.①②③ B.⑤
C.③⑤ D.①⑤
3下列四式中不能化简为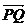 的是( )
的是( )
A.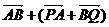 B.
B.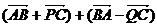
C.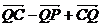 D.
D.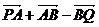
8.已知向量i,j,i=(1,0),j=(0,1)与2i+j垂直的向量为
A.2i-j B.i-2j C.2i+j D.i+2j
[典型例题讲练]
例1四边形ABCD中,=a,=b,=c,=d,且a·b=b·c=c·d=d·a,试问四边形ABCD是什么图形?
变式:在△ABC中,=a,=b,且a·b<0,则△ABC的形状是 ( )
A.锐角三角形 B.直角三角形
C.钝角三角形 D.不能确定
例2若非零向量a和b满足|a+b|=|a-b|.
证明:a⊥b.
变式引申: .已知a+b=c,a-b=d 求证:|a|=|b|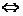 c⊥d
c⊥d
[课堂小结]
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com