
2. 已知圆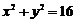 ,
,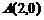 ,若
,若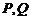 是圆上的动点,且
是圆上的动点,且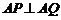 ,求
,求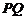 中点的轨迹方程.
中点的轨迹方程.
1. 已知圆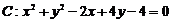 ,问是否存在斜率为1的直线
,问是否存在斜率为1的直线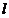 ,使
,使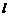 被圆
被圆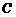 截得弦
截得弦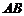 ,以
,以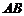 为直径的圆经过原点,若存在,写出直线
为直径的圆经过原点,若存在,写出直线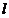 的方程;若不存在,说明理由.
的方程;若不存在,说明理由.
3.已知圆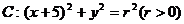 和直线
和直线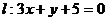 ,若圆
,若圆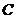 与直线
与直线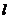 没有公共点,则
没有公共点,则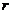 的取值范围是
的取值范围是 .
.
[课后作业]
2.圆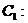
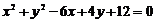 和
和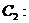
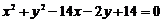 的位置关系为__________________.
的位置关系为__________________.
1.圆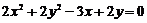 与圆
与圆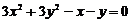 的交点所在直线方程为__________________________________.
的交点所在直线方程为__________________________________.
2.两个圆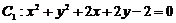 与
与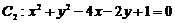 的公切线有且_______________条.
的公切线有且_______________条.
3 若坐标原点在圆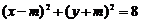 的内部,则实数
的内部,则实数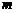 的取值范围是
的取值范围是
4 若直线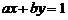 与圆
与圆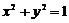 相交,则点
相交,则点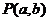 与圆
与圆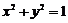 的位置关系是
的位置关系是
§76直线与圆、圆与圆的位置关系(2)
[典型例题]
例1 若圆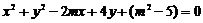 与
与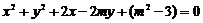 ,当
,当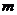 为何值时:(1)两圆外离; (2)两圆外切; (3)两圆相交; (4)两圆内切; (5)两圆内含?
为何值时:(1)两圆外离; (2)两圆外切; (3)两圆相交; (4)两圆内切; (5)两圆内含?
变式 已知圆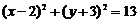 和圆
和圆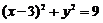 交于
交于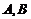 两点,则弦
两点,则弦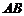 的垂直平分线的方程是_____________________________-.
的垂直平分线的方程是_____________________________-.
例2 求经过两圆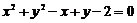 与
与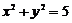 的交点,且圆心在直线
的交点,且圆心在直线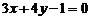 上的圆的方程.
上的圆的方程.
变式 已知两个圆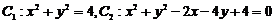 , 直线
, 直线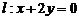 ,求经过
,求经过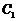 和
和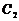 的交点且和
的交点且和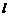 相切的圆的方程.
相切的圆的方程.
[课堂小结]1.两圆的位置关系;2.圆系问题.
[课堂检测]
1.从点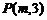 向圆
向圆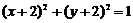 引切线,则切线长的最小值为_________________.
引切线,则切线长的最小值为_________________.
3.直线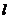 将圆
将圆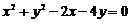 平分,且
平分,且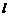 不通过第四象限,则
不通过第四象限,则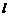 的斜率的取值范围是
的斜率的取值范围是
[典型例题]
例1
已知直线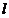 过点
过点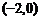 ,当直线
,当直线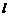 与圆
与圆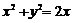 有两个交点时,求直线
有两个交点时,求直线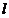 斜率
斜率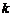 的取值范围?
的取值范围?
变式 能够使得圆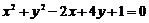
 上恰有两个点到直线
上恰有两个点到直线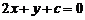 距离等于1的
距离等于1的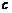 的一个值为( )
的一个值为( )
A.2
B.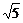 C. 3
D.
C. 3
D.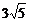


例2 过圆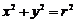
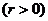 外一点
外一点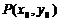 作圆的两条切线,切点分别为
作圆的两条切线,切点分别为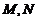 ,证明直线
,证明直线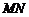 的方程是
的方程是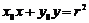 .
.
变式1 从原点向圆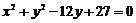 作两条切线,求该圆夹在两条切线间的劣弧长?
作两条切线,求该圆夹在两条切线间的劣弧长?
变式2 圆心为点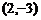 ,且被直线
,且被直线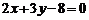 截得的弦长为
截得的弦长为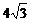 的圆的标准方程为
的圆的标准方程为
[课堂小结]1.直线与圆的三种位置关系;2.圆的切线方程;3.与圆的弦有关的问题
[课堂检测]
2.过点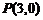 且与圆
且与圆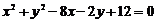 截得的最短弦所在的直线方程是
截得的最短弦所在的直线方程是
1.圆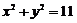 的过点
的过点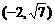 的切线方程为
的切线方程为
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com