
2. 三角形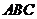 的三边
的三边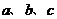 的倒数成等差数列,求证:
的倒数成等差数列,求证: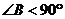 .
.
§94合情推理和演绎推理⑵
[典型例题]
例3. 若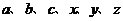 均为实数,
均为实数,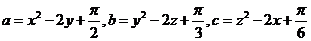 ,
,
求证: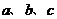 中至少有一个大于0.
中至少有一个大于0.
练习:若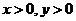 ,且
,且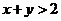 ,求证:
,求证: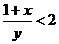 或
或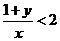 中至少有一个成立.
中至少有一个成立.
例4.若M、N是椭圆C: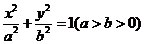 上关于原点对称的两个点,点P是椭圆上任意一点,当直线PM、PN的斜率都存在时,记为
上关于原点对称的两个点,点P是椭圆上任意一点,当直线PM、PN的斜率都存在时,记为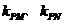 ,那么
,那么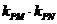 之积是与点P位置无关的定值;试对双曲线
之积是与点P位置无关的定值;试对双曲线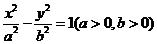 写出具有类似特征的性质,并加以证明 .
写出具有类似特征的性质,并加以证明 .
练习:已知椭圆的两焦点为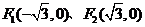 ,离心率为
,离心率为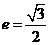 .
.
⑴求此椭圆的方程;
⑵设直线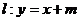 ,若
,若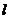 与此椭圆相交于P、Q两点,且PQ等于椭圆的短轴长,求
与此椭圆相交于P、Q两点,且PQ等于椭圆的短轴长,求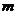 的值;
的值;
⑶以此椭圆的上顶点B为直角顶点作椭圆的内接等腰直角三角形ABC,这样的直角三角形是否存在?若存在,请说明有几个?若不存在,请说明理由 .
[课堂检测]
1.在锐角三角形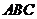 中,求证:
中,求证: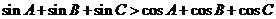 .
.
6.命题“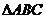 中,若
中,若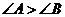 ,则
,则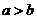 ”的结论否定应该是
.
”的结论否定应该是
.
[典型例题]
例1. 设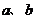 为互不相等的正数,且
为互不相等的正数,且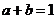 ,分别用分析法、综合法证明:
,分别用分析法、综合法证明: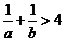
练习:求证: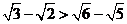
例2.设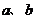 是两相异的正数,求证:关于
是两相异的正数,求证:关于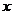 的一元二次方程
的一元二次方程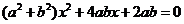 没有实数根.
没有实数根.
练习:设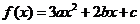 ,若
,若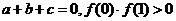 ,
,
⑴求证:方程有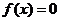 实根;⑵
实根;⑵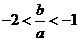 .
.
[课堂检测]
5.“任何三角形的外角都至少有两个钝角”的否定应该是 .
4.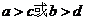 是
是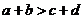 的
条件.
的
条件.
3.用反证法证明“如果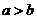 ,那么
,那么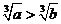 ”反设的内容是
.
”反设的内容是
.
2.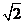
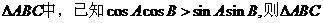 一定是
三角形.
一定是
三角形.
1.命题“对于任意角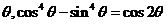 “的证明:
“的证明:
“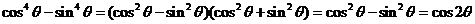 ”过程应用了
.
”过程应用了
.
2. 间接证明:间接证明是不同于直接证明的又一类证明方法,反证法是一种常用的间接证明方法;反证法即从 开始,经过正确的推理,说明假设错误,从而证明了原命题成立,这样的证明方法叫做反证法(归谬法).
[基本训练]
1.直接证明:直接从原命题的条件逐步推得结论成立,这种证明方法叫直接证明;
直接证明的两种基本方法--分析法和综合法
⑴ 综合法 -- ;⑵分析法 -- ;
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com