3．平面向量数量积的坐标表示：

已知a＝(x₁，y₁)，b＝(x₂，y₂)，则a·b＝_____________；记a与b的夹角为θ，则cosθ＝_______________。其中｜a｜=_________。

2．设a与b都是非零向量，e是单位向量，θ₀是a与e夹角，θ是a与b夹角.

①e·a＝a·e＝｜a｜cosθ₀；②a⊥b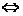a·b＝_____；③当a与b同向时，a·b＝______；

当a与b反向时，a·b＝_______；特别地，a·a＝_______或｜a｜＝_________。④cosθ＝____________；⑤｜a·b｜____｜a｜｜b｜(用不等号填空)。

1．　 知两个非零向量a与b，它们的夹角是θ，则有a · b ＝___________ ，其中夹角θ的取值范围是________。规定0·a＝___________；向量的数量积的结果是一个______。

3.设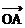=(3，1)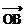，=(-1，2)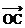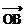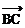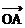，⊥，∥，O为坐标原点，则满足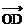+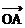=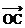的的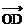坐标是＿＿＿＿　

2.(2005湖北)．已知向量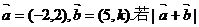不超过5，则k的取值范围是　　　　　

1．平面内给定三个向量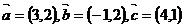，回答下列问题：

(1)求满足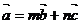的实数m,n；

(2)若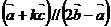，求实数k；

3．已知向量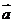=(2x－y+1,x+y－2), 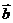=(2,－2),x、y为何值时，　

(1)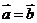；　 (2)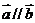

[课后作业]

2．已知三点P(1,1)、A(2,-4)、B(x,-9)在一条直线上，求x的值.

1．若向量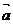=(x+3,x²-3x-4)与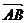相等，其中A(1，2)，B(3，2)，则x=　　　　

5．已知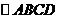中A(3，-2)，B(5，2)，C(-1，4)，则D的坐标为____________

§40　　 平面向量 2 (2)

[典型例题讲练]

例3已知点O(0,0), A(1,2), B(4,5), 及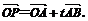问：

(1)　 t 为何值时，P在x轴上? P在第二象限？

(2)　 四边形OABP能否成为平行四边形？若能；求出相应的t值；若不能；请说明理由.

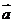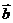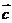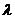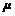变式: 已知＝(3, -1), ＝(-1, 2), ＝(-1,0), 求与，使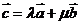

例4．已知向量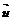＝(x，y)与向量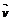＝( y，2y-x)的对应关系用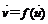表示，

(1) 证明对于任意向量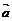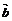，及常数m，n恒有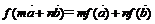成立；

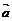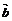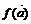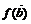(2) 设＝(1，1)，＝(1，0)，求向量及的坐标；

变式引申: 求使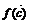＝(p，q) (p，q为常数)的向量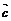的坐标.

[课堂小结]

运用向量的坐标表示，使向量的运算完全代数化，将数与形有机的结合。

[课堂检测]