
(五)、作业布置
必做题:教材P74习题2.2(A组) 第7、8、9题.
选做题:教材P75习题2.2(B组) 第4题.
(四)、归纳小结,强化思想
本小节的目的要求是掌握对数函数的概念、图象和性质.在理解对数函数的定义的基础上,掌握对数函数的图象和性质是本小节的重点.
(三)典型例题
例1.(教材P71例7).
解:(略)
说明:本例主要考察学生对对数函数定义中底数和定义域的限制,加深对对数函数的理解.
巩固练习:(教材731练习2).
(二)、新课教学
(1)对数函数的概念
1.定义:函数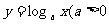 ,且
,且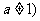 叫做对数函数(logarithmic function)
叫做对数函数(logarithmic function)
其中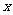 是自变量,函数的定义域是(0,+∞).
是自变量,函数的定义域是(0,+∞).
注意:1 对数函数的定义与指数函数类似,都是形式定义,注意辨别.如: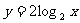 ,
,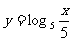 都不是对数函数,而只能称其为对数型函数.
都不是对数函数,而只能称其为对数型函数.
2 对数函数对底数的限制: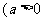 ,且
,且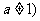 .
.
(2)对数函数的图象和性质
问题:你能类比前面讨论指数函数性质的思路,提出研究对数函数性质的内容和方法吗?
 研究方法:画出函数的图象,结合图象研究函数的性质.
研究方法:画出函数的图象,结合图象研究函数的性质.
研究内容:定义域、值域、特殊点、单调性、最大(小)值、奇偶性.
探索研究:
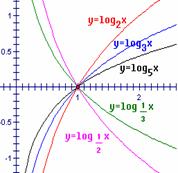
1 在同一坐标系中画出下列对数函数的图象;
(可用描点法,也可借助科学计算器或计算机)
(1)
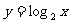 (2)
(2) 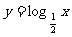
(3)
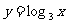 (4)
(4) 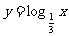
2 类比指数函数图象和性质的研究,研究对数函数的性质并填写如下表格:
|
图象特征 |
函数性质 |
||
 |
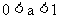 |
 |
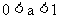 |
|
函数图象都在y轴右侧 |
函数的定义域为(0,+∞) |
||
|
图象关于原点和y轴不对称 |
非奇非偶函数 |
||
|
向y轴正负方向无限延伸 |
函数的值域为R |
||
|
函数图象都过定点(1,0) |
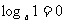 |
||
|
自左向右看, 图象逐渐上升 |
自左向右看, 图象逐渐下降 |
增函数 |
减函数 |
|
第一象限的图象纵坐标都大于0 |
第一象限的图象纵坐标都大于0 |
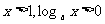 |
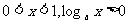 |
|
第二象限的图象纵坐标都小于0 |
第二象限的图象纵坐标都小于0 |
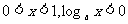 |
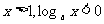 |
3 思考底数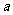 是如何影响函数
是如何影响函数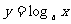 的.(学生独立思考,师生共同总结)
的.(学生独立思考,师生共同总结)
规律:在第一象限内,自左向右,图象对应的对数函数的底数逐渐变大.
(一)、引入课题
1.(知识方法准备)
1 学习指数函数时,对其性质研究了哪些内容,采取怎样的方法?
设计意图:结合指数函数,让学生熟知对于函数性质的研究内容,熟练研究函数性质的方法--借助图象研究性质.
2 对数的定义及其对底数的限制.
设计意图:为讲解对数函数时对底数的限制做准备.
2.(引例)教材引例 处理建议:在教学时,可以让学生利用计算器填写下表:
|
碳14的含量P |
0.5 |
0.3 |
0.1 |
0.01 |
0.001 |
|
生物死亡年数t |
|
|
|
|
|
然后引导学生观察上表,体会“对每一个碳14的含量P的取值,通过对应关系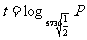 ,生物死亡年数t都有唯一的值与之对应,从而t是P的函数” .
,生物死亡年数t都有唯一的值与之对应,从而t是P的函数” .
(进而引入对数函数的概念)
重点:掌握对数函数的图象和性质.
难点:对数函数的定义,对数函数的图象和性质及应用.
(1)通过具体实例,直观了解对数函数模型所刻画的数量关系,初步理解对数函数的概念,体会对数函数是一类重要的函数模型;
(2)能借助计算器或计算机画出具体对数函数的图象,探索并了解对数函数的单调性与特殊点;
(3)通过比较、对照的方法,引导学生结合图象类比指数函数,探索研究对数函数的性质,培养学生数形结合的思想方法,学会研究函数性质的方法.
必做题:教材P74习题2.2(A组) 第7题.
选做题:教材P75习题2.2(B组) 第4题.
例1.(教材P71例7).
巩固练习:(教材P73练习2).
(1)对数函数的概念
注意;对数函数对底数的限制: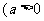 ,且
,且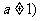 .
.
(2)对数函数的图象和性质
问题:你能类比前面讨论指数函数性质的思路,提出研究对数函数性质的内容和方法吗?
1 在同一坐标系中画出下列对数函数的图象;
(可用描点法,也可借助科学计算器或计算机)
(1) 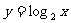 (2)
(2) 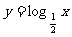
|
|
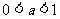 |
 |
|
图 象 |
|
|
|
定义域 |
|
|
|
值域 |
|
|
|
性 质 |
(1) |
|
|
(2) |
(2) |
2 类比指数函数图象和性质的研究,研究对数函数的性质并填写如下表格:
3 思考底数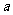 是如何影响函数
是如何影响函数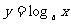 的.(学生独立思考,师生共同总结)
的.(学生独立思考,师生共同总结)
④观察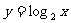 与
与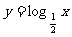 图像有何关系?
图像有何关系?
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com