2、利用换底公式推导下面的结论

(1)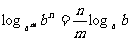；　　　　　 (2)．

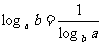课堂练习：P68、练习4

1、试根据对数的定义推导对数的换底公式．

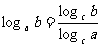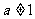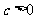　　 (，且；，且；)．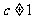

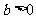(四)作业：教材P74习题2.2 A 组第3、4题

(三)归纳小结，强化思想

本节主要学习了对数的运算性质的推导与应用，在教学中应用多给学生创造尝试、思考、交流、讨论、表达的机会，更应注重渗透转化的思想方法．

(二)新课教学

(1)对数的运算性质

　　　 ①提出问题：根据对数的定义及对数与指数的关系解答下列问题：

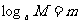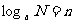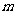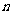设，，试利用、表示·．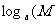

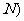(学生独立思考完成解答，教师组织学生讨论评析，进行归纳总结概括得出对数的运算性质1，并引导学生仿此推导其余运算性质)

　　　 ②运算性质：

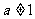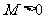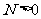　　　 　如果，且，，，那么：

(1)·+．

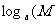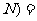
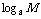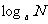可推广到n个数的情形，即；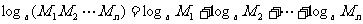

(2)－；

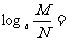
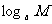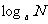(3)　 ；

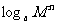
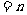
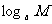
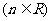(4)

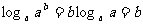
　　　 (引导学生用自然语言叙述上面的三个运算性质)

观察上述性质，提练式子的特征，以加深印象，两个数的积的对数等于两个数对数之和，两个数的商的对数等于两个数对数之差，指数的对数等于指数与对数的积。

3理解并掌握对数的运算性质

进一步了解对数性质的适用条件及形式，并与指数运算性质进行辨析比较，从而巩固对数的运算性质。让学生辨析讨论下面的式子正确吗？

1)

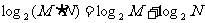
2)

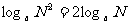
3)

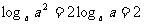
④例题处理

例1：用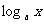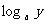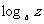，，表示下列各式：

(1)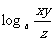　　　　　 (2)

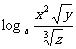
设计意图：在应用过程中进一步理解和掌握对数的运算性质．

例2：求下列各式的值：

(1)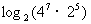　　　　　 (2)

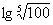
　教师指定两名学生到黑板板演，教师适当的提示和分析，并让学生体会利用对数性质运算时应注意的事项。

课堂练习：

1教材P68练习1~3

设计意图：在练习中反馈学生对对数运算性质掌握的情况，巩固所学知识．

2 已知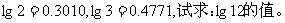

3 试求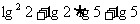：的值。(对换5与2，再试一试)

(一)复习引入

1．　 对数的定义：；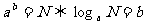

2．　 对数恒等式：，，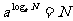

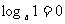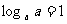
重点：对数的运算性质及其推导过程，以及运用性质进行对数计算

难点：对数的运算性质的推导过程。

(1)理解对数的运算性质；

(2)运用对数的运算性质进行计算和化简。

(1)对数的运算性质有哪些？

(2)辨析讨论下面的式子正确吗？

1)

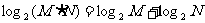
2)

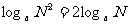
3)

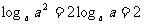
例1：用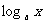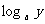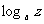，，表示下列各式：(1)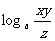；(2)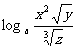

例2：求下列各式的值：(1)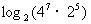；　 (2)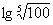

课堂练习：

1教材P68练习1~3

2 已知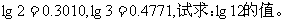

3 试求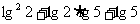：的值。(对换5与2，再试一试)

2．对数恒等式：