(二)、新课讲解

1．我们已经知道，函数是建立在两个非空数集间的一种对应，若将其中的条件“非空数集”弱化为“任意两个非空集合”，按照某种法则可以建立起更为普通的元素之间的对应关系，这种对应就叫映射(板书课题)．

2．先看几个例子，两个集合A、B的元素之间的一些对应关系：

(1)开平方；(2)求正弦；(3)求平方；(4)乘以2．

归纳引出映射概念：

一般地，设A、B是两个非空的集合，如果按某一个确定的对应法则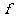，使对于集合A中的任意一个元素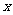，在集合B中都有唯一确定的元素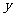与之对应，那么就称对应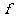：A→B为从集合A到集合B的一个映射．记作“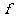：A→B”

说明：

(1)这两个集合有先后顺序，A到B的映射与B到A的映射是截然不同的，其中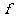表示具体的对应法则，可以用多种形式表述．

(2)“都有唯一”什么意思？

包含两层意思：一是必有一个；二是只有一个，也就是说有且只有一个的意思．

例1．下列哪些对应是从集合A到集合B的映射？

(1)A={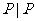是数轴上的点}，B=R，对应关系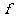：数轴上的点与它所代表的实数对应；

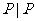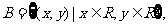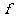(2)A={是平面直角坐标中的点}，对应关系：平面直角坐标系中的点与它的坐标对应；

(3)A={三角形}，B=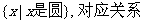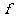：每一个三角形都对应它的内切圆；

(4)A={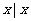是新华中学的班级}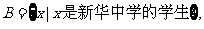，对应关系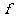：每一个班级都对应班里的学生．

思考：若将(3)中的对应关系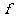改为：每一个圆都对应它的内接三角形；(4)中的对应关系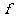改为：每一个学生都对应他的班级，那么对应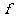：B→A是从集合B到集合A的映射吗？

例2．在下图中，图(1)，(2)，(3)，(4)用箭头所标明的A中元素与B中元素的对应法则，是不是映射？是不是函数关系？

A　　 开平方　　 B　　　　　　　　　　　　　 A　 求正弦　 B

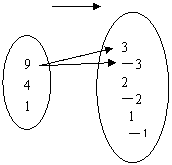
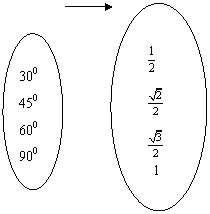
(1)　　　　　　　　　　　　　　　　　　　　　 (2)

A　　 求平方　 B　　　　　　　　　　　　　　 A　 乘以2　 B

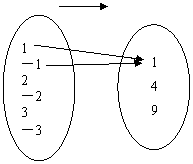
(3)　　　　　　　　　　　　　　　　　　　　　 (4)

巩固深化

1、画图表示集合A到集合B的对应(集合A，B各取4个元素)

已知：(1)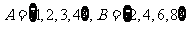，对应法则是“乘以2”；

(2)A=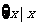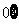＞，B=R，对应法则是“求算术平方根”；

(3)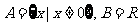，对应法则是“求倒数”；

(4)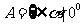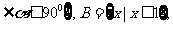＜对应法则是“求余弦”．

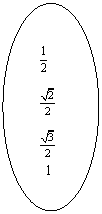
2．在下图中的映射中，A中元素60⁰的象是什么？B中元素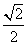的原象是什么？

　　　　　　　　　　　 A　　 求正弦　 B

(一)、复习提问：

复习初中常见的对应关系

1．对于任何一个实数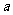，数轴上都有唯一的点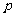和它对应；

2．对于坐标平面内任何一个点A，都有唯一的有序实数对(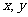)和它对应；

3．对于任意一个三角形，都有唯一确定的面积和它对应；

4．某影院的某场电影的每一张电影票有唯一确定的座位与它对应；

5．函数的概念．

映射的概念

2. 函数推广为映射，只是把函数中的两个数集推广为两个任意的集合；

3 通过实例进一步理解映射的概念；

4 会利用映射的概念来判断一些简单的“对应关系”是否是映射，一一映射

1. 了解映射的概念及表示方法

2．在下图中的映射中，A中元素60⁰的象是什么？B中元素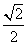的原象是什么？

　　　　　　　　　　　 A　　 求正弦　 B

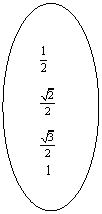
1、画图表示集合A到集合B的对应(集合A，B各取4个元素)

已知：(1)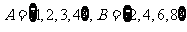，对应法则是“乘以2”；

(2)A=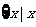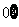＞，B=R，对应法则是“求算术平方根”；

(3)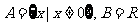，对应法则是“求倒数”；

(4)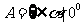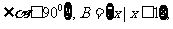＜对应法则是“求余弦”．

5．函数的概念．

二新课预习

映射的概念：

例1．下列哪些对应是从集合A到集合B的映射？

(1)A={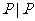是数轴上的点}，B=R，对应关系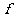：数轴上的点与它所代表的实数对应；

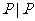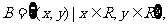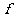(2)A={是平面直角坐标中的点}，对应关系：平面直角坐标系中的点与它的坐标对应；

(3)A={三角形}，B=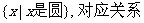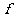：每一个三角形都对应它的内切圆；

(4)A={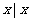是新华中学的班级}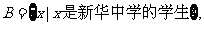，对应关系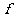：每一个班级都对应班里的学生．

例2．在下图中，图(1)，(2)，(3)，(4)用箭头所标明的A中元素与B中元素的对应法则，是不是映射？是不是函数关系？

A　　 开平方　　 B　　　　　　　　　　　　　 A　 求正弦　 B

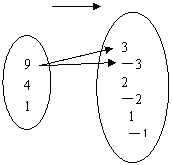
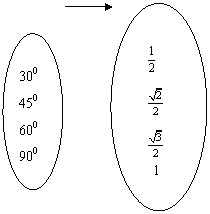
(1)　　　　　　　　　　　　　　　　　　　　　 (2)

A　　 求平方　 B　　　　　　　　　　　　　　 A　 乘以2　 B

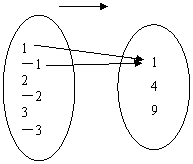
(3)　　　　　　　　　　　　　　　　　　　　　 (4)

练习

4．某影院的某场电影的每一张电影票有唯一确定的座位与它对应；

3．对于任意一个三角形，都有唯一确定的面积和它对应；