例3、给出下列四个对应的关系

①A=N*,B=Z,f:x→y=2x－3；

②A={1，2，3，4，5，6}，B={y|y∈N*,y≤5}，f:x→y=|x－1|；

③A={x|x≥2}，B={y|y=x²－4x+3}，f:x→y=x－3；

④A=N,B={y∈N*|y=2x－1，x∈N*}，f:x→y=2x－1。

上述四个对应中是函数的有(　　 )

A.①　　　　　　　　　　 B.①③　　　　　　　　 C.②③　　　　　　　　 D.③④

思维分析：判断两个集合之间的对应是否构成函数，首先应判断能否构成映射，且构成映射的两个集合之间对应必须是非空数集之间的对应。

[选修延伸]

求映射的个数问题

例4、已知A={a,b,c}，B={－1，0，1},映射f:A→B满足f(a)+f(b)=f(c)，求映射f: A→B的个数。

思维分析：可让A中元素在f下对应B中的一个、两个或三个元素，并且满足f(a)+f(b)=f(c)，需分类讨论。

追踪训练

1、下列对应是A到B上的映射的是(　 )

A.A=N*,B=N*,f:x→|x－3|

B.A=N*，B={－1,1, －2}，f:x→(－1)^x

C.A=Z,B=Q,f:x→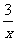

D.A=N*，B=R，f:x→x的平方根

例2、已知集合A=R，B={(x,y)|x,y∈R}，f:A→B是从A到B的映射，f:x→(x+1,x²+1)，求A中的元素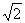在B中的象和B中元素(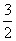,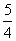)在A中的原象。

思维分析：将x=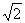代入对应关系，可求出其在B中对应元素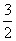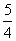，(,)在A中对应的元素可通过列方程组解出。

例1、下列集合M到P的对应f是映射的是(　　 )

A.M={－2，0，2}，P={－1，0，4},f：M中数的平方

B.M={0，1}，P={－1，0，1}，f:M中数的平方根

C.M=Z，P=Q，f:M中数的倒数。

D.M=R，P=R⁺，f:M中数的平方

5、函数f(x)=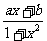是定义在(－1，1)上的奇函数，且f()=.

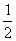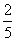(1)确定函数f(x)的解析式；

(2)用定义证明f(x)在(－1，1)上是增函数；

(3)解不等式f(t－1)+f(t)<0；

4、已知f(x)是偶函数，g(x)是奇函数，它们的定义域均为{x|x∈R且x≠±1}，若f(x)+g(x)=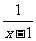，则f(x)=________,g(x)=__________.

3、设f(x)在R上是偶函数，在区间(－∞，0)上递增，且有f(2a²+a+1)<f(3a²－2a+1)，求a的取值范围。

2、下列函数中，在区间(－∞，0)上为增函数的是(　　 )

A.y=1+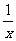　　　　　　　　　　　　　 B.y=－(x+1)²

C.y=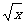　　　　　　　　　　　　　　 D.y=x³

例4、设f(x)是定义在[－2，2]上的偶函数，当x≥0时，f(x)单调递减，若f(1－m)<f(m)成立，求m的取值范围。

追踪训练

1、函数f(x)=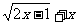的值域是(　　 )

A.[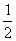，+∞)　　　　　　　　　　　　　　 B.(－∞，]　　　　　　　　　　

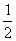C.(0,+∞)　　　　　　　　　　　　　　　　　 D.[1,+ ∞)

例3、已知y=f(x)是偶函数，且图象与x轴四个交点，则方程f(x)=0的所有实根之和是(　　 )

A.4　　　　　　　　　　　 B.2　　　　　　　　　　　 C.0　　　　　　　　　　　 D.不知解析式不能确定

例2、求函数y=的单调区间，并对其中一种情况证明。

思维分析：要求出y=的单调区间，首先求出定义域，然后利用复合函数的判定方法判断.