
6.已知数列{an}中a3=2,a7=1,又数列{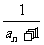 }为等差数列,则a11等于( B
)
}为等差数列,则a11等于( B
)
A.0 B.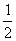 C.
C.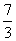 D.-1
D.-1

5.在-1和8之间插入两个数a,b,使这四个数成等差数列,则a=______,b=______.
[解析]d=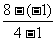 =3∴a=-1+3=2,b=2+3=5
=3∴a=-1+3=2,b=2+3=5
[答案]2 5
4.在等差数列{an}中,若a3=50,a5=30,则a7=______.
 [解法一] d=
[解法一] d=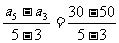 =-10∴a7=a3+(7-3)d=50-40=10
=-10∴a7=a3+(7-3)d=50-40=10
[解法二] 由2a5=a3+a7得a7=2a5-a3=2×30-50=10
[答案]10
3.已知等差数列{an}的前3项依次为a-1,a+1,2a+3,则此数列的通项an为( B )
A.2n-5 B.2n-3
C.2n-1 D.2n+1
2.等差数列{an}中,a2=-5,d=3,则a1为(B)
A.-9 B.-8 C.-7 D.-4
1.数列{an}的通项公式an=2n+5,则此数列( A )
A.是公差为2的等差数列
B.是公差为5的等差数列
C.是首项为5的等差数列
D.是公差为n的等差数列
4.已知数列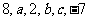 是等差数列,求未知项
是等差数列,求未知项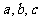 的值。
的值。
[解]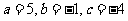
[选修延伸]
[例4]在等差数列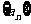 中,已知
中,已知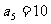 ,
,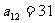 ,求
,求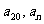
分析: 先根据两个独立的条件解出两个量a1和d,进而再写出an的表达式.几个独立的条件就可以解出几个未知量,这是方程组的重要应用.
[解法一]:
∵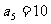 ,
,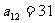 ,则
,则
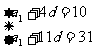
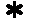
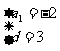
∴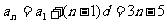

思考:在此题中,有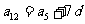 ,思考,能否不求首项
,思考,能否不求首项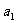 ,而将
,而将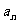 求出?
求出?
[解法二]:
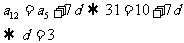
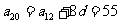
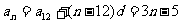
思维点拔:
等差数列的通项公式涉及到四个量a1、an、n、d,用方程的观点知三求一。列方程组求基本量是解决等差数列问题的常用方法,注意通项公式更一般的形式: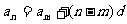
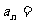
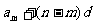
[例5]若 ,则
,则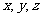 成等差数列。
成等差数列。
[证明]由 得
得
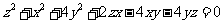 ,
,
即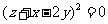 ,
,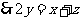 ,
,
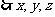 成等差数列。
成等差数列。
思维点拔:
当已知a、b、c成等差数列时,通常采用2b=a+c作为解决问题的出发点.
[追踪训练二]:
3.已知下列数列是等差数列,试在括号内填上适当的数:
(1)( ),5,10;
(2)1,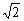 ,( );
,( );
(3)31,( ),( ),10.
2.目前男子举重比赛共有10个级别,除108公斤以上级外,其余的9个级别从小到大依次为(单位:kg)54,59,64,70,76,83,91,99,108,这个数列是等差数列吗?
1.判断下列数列是否为等差数列: (1)-1,-1,-1,-1,-1;
(2)1,12,13,14;
(3)1,0,1,0,1,0;
(4)2,4,6,8,10,12;
(5)7,12,17,22,27.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com