
3.若数列{an}满足a1=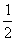 ,an=1-
,an=1-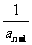 ,n≥2,n∈N*,则a2003等于( )
,n≥2,n∈N*,则a2003等于( )
A.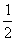 B.-1 C.2 D.1
B.-1 C.2 D.1
2.数列{-2n2+29n+3}中最大项的值是( )
A.107 B.108 C.108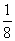 D.109
D.109
1.已知数列{an}的首项a1=1,且
an=2an-1+1(n≥2),则a5为( )
A.7 B.15 C.30 D.31
4.设凸n边形的对角线条数为f(n),则f(3)=______;f(n+1)=______用f(n)表示.
[选修延伸]
[例4]已知数列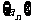 的通项为
的通项为
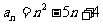 ,问:
,问:
(1).数列中有多少项为负数?
(2).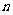 为何值时,
为何值时,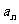 有最小值?并求此最小值.
有最小值?并求此最小值.
分析:数列的通项公式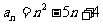 可看成
可看成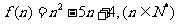 ,利用二次函数的性质解决问题.
,利用二次函数的性质解决问题.
[解]
点评:数列的项与项数之间构成特殊的函数关系,用函数的有关知识解决问题时,要考虑定义域为正整数这一约束条件.
 [追踪训练二]
[追踪训练二]
3.数列1,3,6,10,15,……的递推公式是( )
A.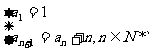
B.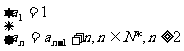
C.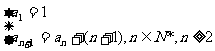
D.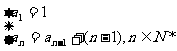
2.已知数列{an}满足a1>0,且an+1=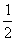 an,则数列{an}是
( )
an,则数列{an}是
( )
A.递增数列 B.递减数列
C.常数列 D.摆动数列
1.已知an+1=an+3,则数列{an}是( )
A.递增数列 B.递减数列
C.常数列 D.摆动数列
3.递推数列:如果已知数列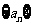 的前一项(或前几项),且任意一项
的前一项(或前几项),且任意一项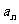 与它的前一项
与它的前一项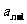 (或前几项)间的关系可以用一个公式来表示,则这个数列叫递推数列,这个公式叫这个数列的递推公式.递推公式是给出数列的一种重要方式.
(或前几项)间的关系可以用一个公式来表示,则这个数列叫递推数列,这个公式叫这个数列的递推公式.递推公式是给出数列的一种重要方式.
[精典范例]
[例1]写出下面数列的一个通项公式,使它的前4项分别是下列各数:
(1)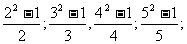
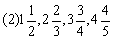
(3)9,99,999,9999
 [解]
[解]
[例2]已知数列{an}的递推公式是
an+2=3an+1-2an,且a1=1,a2=3,求数列的前5项,并推测数列{an}的通项公式.
[解]
[例3]设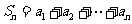 ,其中
,其中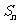 为数列的前
为数列的前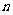 项和,已知数列
项和,已知数列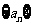 的前
的前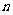 项和
项和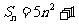 ,求该数列的通项公式。
,求该数列的通项公式。
分析:由于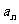 与
与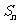 的关系是
的关系是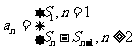 因而已知
因而已知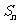 求
求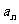 时,常用的解题策略是先求
时,常用的解题策略是先求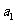 再将
再将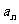 用
用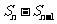 表示,但由于
表示,但由于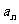 =
=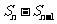 只能求出数列的第二项及以后各项,故特别要注意验证
只能求出数列的第二项及以后各项,故特别要注意验证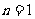 的情形是否满足
的情形是否满足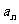 =
=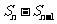 ,若满足,则
,若满足,则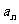 是关于
是关于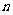 的一个式子,否则写成分段函数的形式.
的一个式子,否则写成分段函数的形式.
[解]
[追踪训练一]
2.数列的分类:
按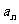 的增减分类:
的增减分类:
(1)___________: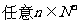 ,总有
,总有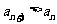 ;
;
(2)___________: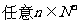 ,总有
,总有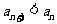 ;
;
(3)_____________ 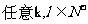 ,
,
有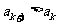 ,也有
,也有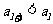 ,
,
例如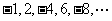 ;
;
(4)________: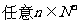 ,
,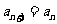 ;
;
(5)____________:存在正整数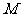 使
使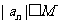 ;
;
(6)____________:对任意正整数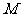 总存在
总存在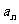 使
使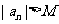 .
.
1.数列的一般形式:________________,或简记为_____,其中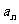 是数列的第___项。
是数列的第___项。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com