
2. △ABC中若sin(A+B)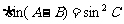 ,则△ABC是( B )
,则△ABC是( B )
A 锐角三角形 B 直角三角形
C 钝角三角形 D 等腰三角形
[例6]已知圆内接四边形ABCD的边长分别为AB=2,BC=6,CD=DA=4,求四边形ABCD的面积。
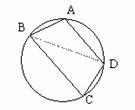
分析:连结对角线BD,将四边形面积转化为三角形面积来求,而要求三角形面积,需求出∠A、∠C,这可由余弦定理列方程求得。
[解]
四边形ABCD的面积S=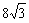 .
.
注:在应用正弦定理解题时要注意方程思想的运
追踪训练一
1. △ABC中a=6,b=6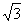 A=30°则边C=( C )
A=30°则边C=( C )
A、6 B、、12 C、6或12 D、6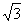
[例2]△ABC中,已知:AB=2,BC=1,CA=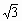 ,分别在边AB、BC、CA上取点D、E、F,使△DEF是等边三角形.设∠FEC=α,问sinα为何值时,△DEF的边长最短?并求出最短边的长。
,分别在边AB、BC、CA上取点D、E、F,使△DEF是等边三角形.设∠FEC=α,问sinα为何值时,△DEF的边长最短?并求出最短边的长。
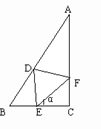
分析:要求最短边的长,需建立边长关于角α的目标函数。
[解]设△DEF的边长为x,显然∠C=90°,∠B=60°,故EC=x·cosα。因为∠DEC=∠DEF+α=∠EDB+∠B,所以∠EDB=α。在△BDE中,由正弦定理得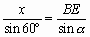 ,
,
 所以
所以 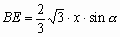 ,因为BE+EC=BC,所以
,因为BE+EC=BC,所以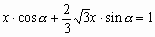 ,
,
所以 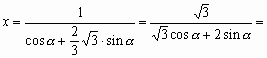
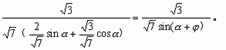 当
当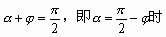 ,
,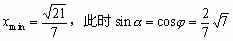 。
。
注:在三角形中,已知两角一边求其它边,自然应联想到正弦定理。
[例3]在△ABC中,已知sinB=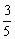 ,
,
cosA=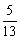 , 试求cosC的值。
, 试求cosC的值。
[解]由cosA=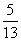 ,得sinA=
,得sinA=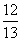 ,
,
∵ sinB<sinA, ∴ B中能是锐角
∴ cosB=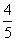 ,
,
又
cosC= - cos(A + B)=sinAsinB – cosAcosB=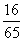 .
.
[例4]在△ABC中,已知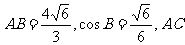 边上的中线BD=
边上的中线BD=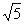 ,求sinA的值.
,求sinA的值.
分析:本题主要考查正弦定理、余弦定理等基础知识,同时考查利用三角公式进行恒等变形
的技能和运算能力.
[解]设E为BC的中点,连接DE,则DE//AB,且DE=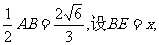
在△BDE中利用余弦定理可得:
BD2=BE2+ED2-2BE·EDcosBED,
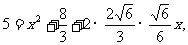
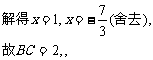
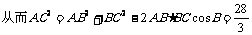
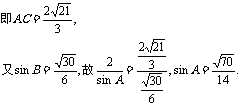
[例5]在ΔABC中,角A、B、C所对的边分别为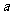 、b、c,且
、b、c,且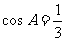 .
.
(Ⅰ)求 的值;
的值;
(Ⅱ)若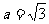 ,求bc的最大值.
,求bc的最大值.
[解](Ⅰ)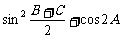 =
=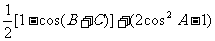
=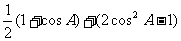
=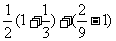 =
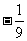
= 
(Ⅱ) ∵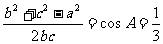
 ∴
∴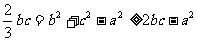 ,
,
又∵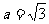
∴
当且仅当 b=c=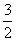 时,bc=
时,bc=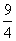 ,故bc的最大值是
,故bc的最大值是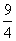 .
.
[例1]根据下列条件判断三角形ABC的形状:
(1) 若a2tanB=b2tanA;
(2) b2sin2C + c2sin2B=2bccosBcosC;
(3) (3)(sinA + sinB + sinC) – (cosA + cosB + cosC)=1.
[解](1)由已知及正弦定理得
(2RsinA)2
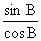 = (2RsinB)2
= (2RsinB)2 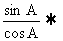
2sinAcosA=2sinBcosB sin2A=sin2B
sin2A=sin2B
2cos(A + B)sin(A – B)=0
∴ A + B=90o 或 A – B=0
所以△ABC是等腰三角形或直角三角形.
(2)由正弦定理得
sin2Bsin2C=sinBsinCcosBcosC
∵ sinBsinC≠0,
∴ sinBsinC=cosBcosC,
即 cos(B + C)=0, ∴ B + C=90o, A=90o,
故△ABC是直角三角形.
(3)(sinA +
sinB + sinC) – (cosA + cosB + cosC)=1 [2sin
[2sin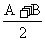 cos
cos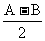 + sin(A + B)] – [2cos
+ sin(A + B)] – [2cos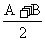 cos
cos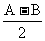 + 2cos2
+ 2cos2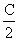 - 1]=0
- 1]=0
 [2sin
[2sin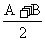 cos
cos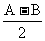 + sin(A + B)] – 2cos
+ sin(A + B)] – 2cos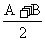 cos
cos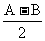 - 2sin2
- 2sin2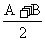 =0
=0 (sin
(sin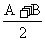 - cos
- cos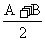 )(cos
)(cos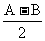 - sin
- sin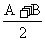 )=0
)=0 sin(
sin(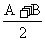 -
- 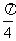 )sin
)sin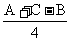 sin
sin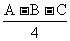 =0
=0
 △ABC是Rt△.
△ABC是Rt△.
3.两艘快艇在水面上一前一后前进,后一艘快艇的速度是前一艘的两倍,前一艘快艇突然向与原前进方向成300角行驶,若后一快艇需想在最短的时间内赶上前艇,则它行驶的方向应与原方向的夹角为 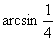

2.在△ABC中,若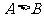 ,则
,则 与
与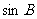 的大小关系是 ( A
)
的大小关系是 ( A
)
A 大于 B 大于等于
C 小于 D 小于等于
解: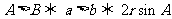
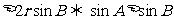
1.我国潜艇外出执行任务,在向正东方向航行时,测得某国的雷达站在潜艇的东偏北300方向的100n mile处,已知该国的雷达扫描半径为70n mile,若我国潜艇不改变航向,则行驶多少路程后会有暴露目标?( B )
A 50
B 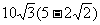
C
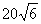 D
D 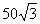
3.在△ABC中,若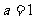 ,B=450,△ABC的面积为2,那么,△ABC的外接圆直径为
,B=450,△ABC的面积为2,那么,△ABC的外接圆直径为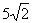
[选修延伸]
[例3]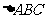 中,若已知三边为连续正整数,最大角为钝角,
中,若已知三边为连续正整数,最大角为钝角,
① 求最大角的余弦值;
② 求以此最大角为内角,夹此角两边之和为4的平行四边形的最大面积.
[解]①设三边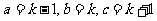 ,
, 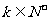 且
且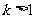 ,
,
∵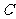 为钝角,
为钝角,
∴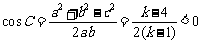 ,
,
解得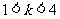 ,
,
∵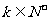 , ∴
, ∴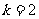 或
或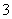 ,但
,但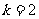 时不能构成三角形应舍去,
时不能构成三角形应舍去,
当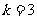 时,
时,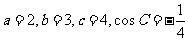 ;
;
②设夹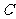 角的两边为
角的两边为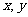 ,
,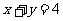 ,
,
 所以,
所以,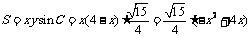 ,当
,当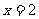 时,
时,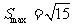 .
.
追踪训练二
2. 从200m高的电视塔顶A测得地面上某两点B,C的俯角分别为30°和
45°,∠BAC=45°,求这两个点之间的距离.
答案: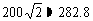
1. 如图,用两根绳子牵引重为F1=100N的物体,两根绳子拉力分别为F2,F3,保持平衡.如果F2=80N,F2与F3夹角α=135°.
(1)求F3的大小(精确到1N);
(2)求F3与F1的夹角β的值
(精确到0.1°).

答案:(1)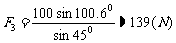
(2)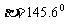
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com