
1.掌握用“错位相减”的方法推导等比数列的前n项和公式,掌握等比数列的前n项和公式
5.已知数列满足a1=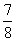 ,且an+1=
,且an+1=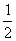 an+
an+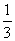 ,n∈N*
,n∈N*
(1)求证{an-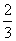 }是等比数列.
}是等比数列.
(2)求数列{an}的通项公式.
[解]
(1)[证明] 由an+1 =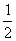 an+
an+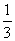 得
得
 an+1-
an+1-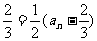 又an-
又an-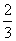 ≠0
≠0
∴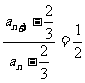
即,数列{an-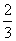 }构成等比数列.
}构成等比数列.
(2)由(1)知an-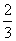 =(a1-
=(a1-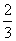 )(
)(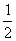 )n-1,
)n-1,
且a1=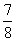
即an=(a1-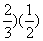 n-1+
n-1+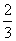
=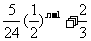 =
=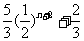
|
4.公差不为0的等差数列第二、三、六项构成等比数列,则公比为 ( C )
A.1 B.2 C.3 D.4
3.已知一个直角三角形三边的长成等比数列,则( C )
A.三边边长之比为3∶4∶5
B.三边边长之比为1∶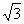 ∶3
∶3
C.较小锐角的正弦为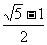
D.较大锐角的正弦为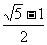
2.在各项都为正数的等比数列{an}中,若a5·a6=9,则log3a1+log3a2+log3a3+…+log3a10等于( B )
A.8 B.10 C.12 D.2+log35
1.在等比数列{an}中,若a2·a8=36,a3+a7=15,则公比q值的可能个数为( D )
A.1 B.2 C.3 D.4
5.已知等差数列{an}的公差d≠0,且a1,a3,a9成等比数列,则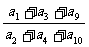 的值为
的值为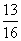 .
.
[选修延伸]
[例3]在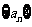 中,
中,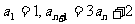 ,试求
,试求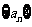 的通项
的通项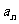
[解]设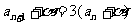 则
则
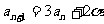 可得
可得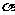 =1
=1
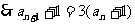 ,
,
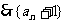 为等比数列,首项为
为等比数列,首项为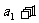 =2,公比为3
=2,公比为3
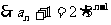 ,
,
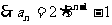
[例4]在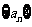 中,
中,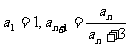 ,试求
,试求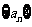 的通项
的通项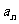
[解]原式可变为: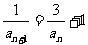 ,
,
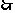 可构造为
可构造为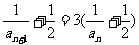
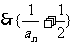 为等比数列,首项
为等比数列,首项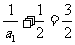 ,公比3
,公比3
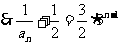 ,
,
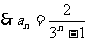
[例5]在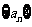 中
中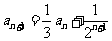 ,
,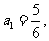 求{
求{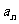 }的通项
}的通项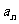
[解]法一:
原式变形为: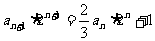 ,设
,设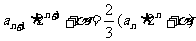 ,
,
即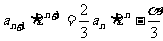 ,
,
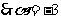 ,
,
即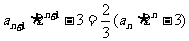 ,
,
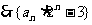 为等比数列,首项
为等比数列,首项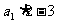 =
=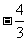 ,公比
,公比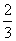
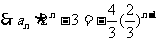 ,
,

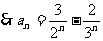
法二:
设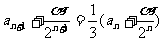 ,即
,即
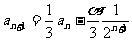
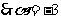
即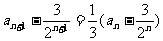 ,
,
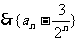 为等比数列,
为等比数列,
首项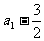 =
=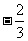 ,公比
,公比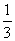 ,
,
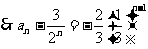 ,
,
追踪训练二
4.已知{an}是等比数列,且an>0,a2a4+2a3a5+a4a6=25,那么a3+a5的值等于( A )
A.5 B.10 C.15 D.20
3.2,x,y,z,162是成等比数列的五个正整数,则z的值等于( A )
A.54 B.27 C.9 D.3
2.在等比数列{an}中,已知a5=-2,则这个数列的前9项的乘积等于( B )
A.512 B.-512 C.256 D.-256
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com