
4.已知数列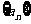 满足
满足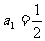 ,
,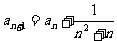 ,求
,求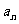 .
.
 [解]由条件知:
[解]由条件知: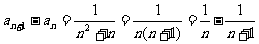
分别令 ,代入上式得
,代入上式得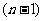 个等式累加之,即
个等式累加之,即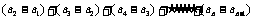
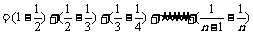 所以
所以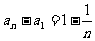
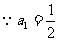 ,
,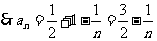
3.设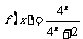 ,利用课本中推导等差数列前
,利用课本中推导等差数列前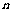 项和方法,求
项和方法,求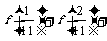 …
…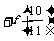 的值为 5
.
的值为 5
.
2.三角形三个边长组成等差数列,周长为36,内切圆周长为6π,则此三角形是( D )A.正三角形 B.等腰直角三角形C.等腰三角形,但不是直角三角形
D.直角三角形,但不是等腰三角形
1.在等差数列中,前n项的和为Sn,若Sm=2n,Sn=2m,(m、n∈N且m≠n),则公差d的值为( A )
A.-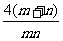 B.-
B.-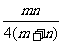
C.-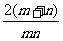 D. -
D. -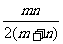
5.时钟在1点钟的时候敲一下,在2点钟的时候敲2下……在12点钟的时候敲12下,中间每半点钟也敲一下.一昼夜内它一共敲多少下?
[答案]一昼夜内它一共敲180下
[选修延伸]
[例4]已知数列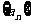 的通项公式为
的通项公式为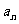 =
=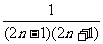 ,求它的前
,求它的前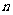 项和.
项和.
分析:我们先看通项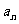 =
=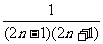 ,然后将其分裂成
,然后将其分裂成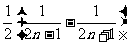 ,再求和.
,再求和.
[解]
∵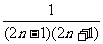 =
=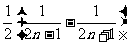
∴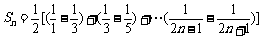
=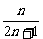
点评: 如果数列的通项公式可转化为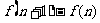 形式,常采用裂项求和的方法.特别地,当数列形如
形式,常采用裂项求和的方法.特别地,当数列形如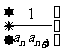 ,其中
,其中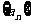 是等差数列,可尝试采用此法.
是等差数列,可尝试采用此法.
常用裂项技巧如: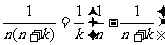 ,
,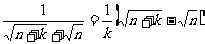 等.
等.
[例5]已知数列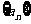 满足
满足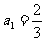 ,
,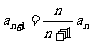 ,求
,求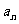 .
.
[解]由条件知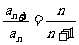 ,分别令
,分别令 ,代入上式得
,代入上式得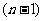 个等式累乘之,即
个等式累乘之,即
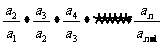
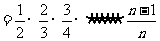
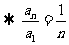
又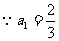 ,
,
追踪训练二
4.某钢材库新到200根相同的圆钢,要把它们堆放成正三角形垛(如图),并使剩余的圆钢尽可能地少,那么将剩余多少根圆钢?

[答案]将剩余10根圆钢
3. 已知一个凸多边形的内角度数组成公差为5°的等差数列,且最小角为120°,问它是几边形.
已知一个凸多边形的内角度数组成公差为5°的等差数列,且最小角为120°,问它是几边形.
[答案]9边形
2. 已知等差数列{an}满足a1+a2+…+a101=0,则有( C ).
A.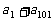 >0 B.
>0 B.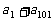 <0
<0
C.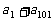 =0 D.
=0 D.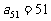
1. 已知an = 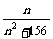 (n∈N*), 则数列{an}的最大项是( C )
(n∈N*), 则数列{an}的最大项是( C )
A.第12项 B.第13项
C.第12项或第13项 D.不存在
59.95=20.05+(n-1)×0.1,
所以n=400.
显然,各圈的周长组成一个首项为40.1π,公差为0.2π,项数为400的等差数列.根据等差数列的求和公式,得
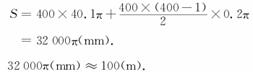
答 满盘时卫生纸的长度约为100m.
[例3])教育储蓄是一种零存整取定期储蓄存款,它享受整存整取利率,利息免税.教育储蓄的对象为在校小学四年级(含四年级)以上的学生.假设零存整取3年期教育储蓄的月利率为2.1‰.
(1)欲在3年后一次支取本息合计2万元,每月大约存入多少元?
(2)零存整取3年期教育储蓄每月至多存入多少元?此时3年后本息合计约为多少?(精确到1元)
[解](1)设每月存A元,则有
A(1+2.1‰)+A(1+2×2.1‰)+…+A(1+36×2.1‰)=20000
利用等差数列求和公式,得
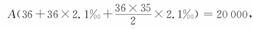
解得A≈535(元)
(2)由于教育储蓄的存款总额不超过2万元,所以3年期教育储蓄每月至多可存入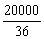 ≈555(元).这样,3年后的本息和为
≈555(元).这样,3年后的本息和为
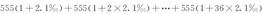
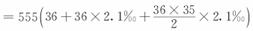
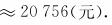
答 欲在3年后一次支取本息2万元,每月大约存入535元.3年期教育储蓄每月至多存入555元,3年后本息合计约20756元.
追踪训练一
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com