
解: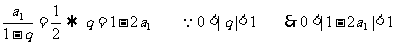
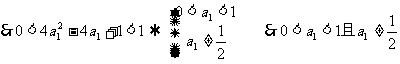
解:设首项为a ,公比为 q,( | q | <1 ) 则
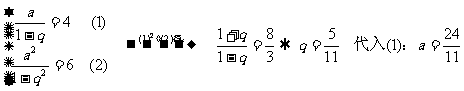
∴各项的立方和: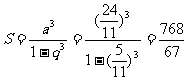
2. 混循环小数化分数:将一个循环节连同不循环部分的数减去不循环部分所得的差作分子,分母是99…900…0,其中9的个数与一个循环节的个数相同,0的个数和不循环部分的数字个数相同。
1. 纯循环小数化分数:将一个循环节的数作分子,分母是99……9,其中9的个数是循环节数字的个数。
2.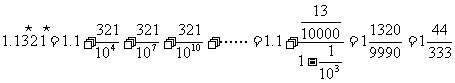
小结法则:
1.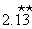 2.
2.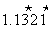
解:1.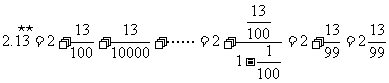
解: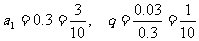
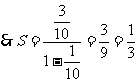
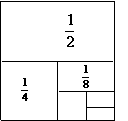 解:公比
解:公比 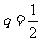 ,
, 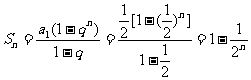
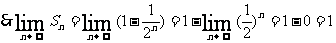
解释:“无穷递缩等比数列”
1°
当 时,数列为无穷递缩等比数列相对于以前求和是求有限项(n项)
时,数列为无穷递缩等比数列相对于以前求和是求有限项(n项)
2° 当 | q | <1时,数列单调递减,故称“递缩”
3° 数列{an}本身成GP
小结:无穷递缩等比数列前n项和是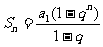
当 时,
时, 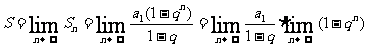
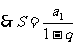 其意义与有限和是不一样的
其意义与有限和是不一样的
2.作业:(1)课本P156习题10.7 :1,2,3
(2)思考:相互独立事件与互斥事件的比较。(表)
1.小结:相互独立事件,相互独立事件同时发生的概率乘法公式。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com