4．已知数列{a_n}为等比数列，

(1)若a_n＞0，且a₂a₄+2a₃a₅+a₄a₆＝25，

求a₃+a₅.

(2)a₁+a₂+a₃＝7，a₁a₂a₃＝8，求a_n.

3．已知等比数列{a_n}的公比q=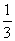－,则=___ ___.

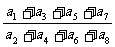2．在等比数列中，已知首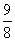项为，末项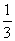为,公比为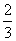，则项数n等于___ __.

1．在等比数列{a_n}中，a₃·a₄·a₅＝3，a₆·a₇·a₈＝24，则a₉·a₁₀·a₁₁的值等于(　 )

A.48　　　　 　 B.72　　 C.144　　　 D.192

3.已知数列{a_n}是公比q≠±1的等比数列，则在{a_n+a_n+1},{a_n+1－a_n}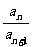，{}na_n这四个数列中，是等比数列的有(　　 )

A.1个 　 　　B.2个　 C.3个　　　 D.4个

[选修延伸]

[例5]成等差数列的三个正数之和为15，若这三个数分别加上1，3，9后又成等比数列，求这三个数.

[解]

[例6]已知数列{a_n}满足：lga_n＝3n+5，试用定义证明{a_n}是等比数列.

[证明]

[点评] 若{a_n}是等差数列，b_n＝b^a_n可以证明数列{b_n}为等比数列，反之若{a_n}为等比数列且a_n＞0，则可证明{lga_n}为等差数列.

追踪训练二

2. 数列m,m,m,…m, (　　 )

A. 一定是等比数列　　　　　

B.既是等差数列又是等比数列　

C.一定是等差数列，不一定是等比数列　　

D.既不是等差数列，又不是等比数列

1. 求下列等比数列的公比、第5项和第n项：

(1)2，6，18，54，…；　

(2)7，，，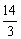

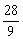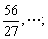
(3)0.3，－0.09，0.027，－0.0081，…；

(4)5，　，，.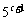

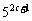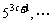5．证明数列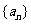为等比数列：

⑴定义：证明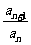=常数；

⑵中项性质：；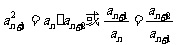

[精典范例]

[例1]判断下列数列是否为等比数列：

(1)1，1，1，1，1；

(2)0，1，2，4，8；

(3)1，，，，.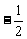

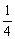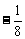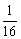[解]

[例2]求出下列等比数列中的未知项：

(1)2，a，8；

(2)－4，b，c，．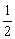

[解]

[例3]在等比数列{a_n}中，

(1)已知a₁＝3，q＝－2，求a₆；

(2)已知a₃＝20，a₆＝160，求a_n．

[解]

[例4]在243和3中间插入3个数，使这5个数成等比数列．

[解]

追踪训练一

4.等比中项的定义：如果a，G，b成等比数列，那么G叫做a与b的等比中项.且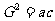

3．既是等差又是等比数列的数列：_______．