
2.了解等差数列的一些性质,并会用它们解决一些相关问题;
1.进一步熟练掌握等差数列的通项公式和前n项和公式;
5.已知数列{an}的前n项和是Sn=32n-n2,求数列{|an|}的前n项和Sn′.
[解] ∵a1=S1=32×1-12=31,当n≥2时,an=Sn-Sn-1=33-2n,
又由an>0,得n<16.5,即{an}前16项为正,以后皆负.
∴当n≤16时,Sn′=|a1|+|a2|+…+|an|=a1+a2+…+an=33n-n2.
当n>16时,Sn′=a1+a2+…+a16-a17-a18-…-an=S16-(Sn-S16)=2S16-Sn=512-32n+n2.
∴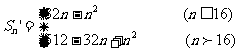

|
4.一个等差数列的前12项的和为354,前12项中,偶数项和与奇数项和之比为32∶27,则公差d等于___5___.
[解析]由已知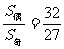 ,又S偶+S奇=354
,又S偶+S奇=354
∴S偶=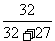 (S偶+S奇)=192 S奇=162 d=
(S偶+S奇)=192 S奇=162 d=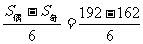 =5 [答案]5
=5 [答案]5
3.等差数列{an}的通项公式是an=2n+1,由bn=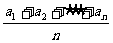 (n∈N*)确定的数列{bn}的前n项和是( A )
(n∈N*)确定的数列{bn}的前n项和是( A )
A.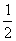 n(n+5) B.
n(n+5) B.
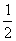 n(n+4)
n(n+4)
C. 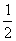 n(2n+7) D.n(n+2)
n(2n+7) D.n(n+2)
2.在项数为2n+1的等差数列中,所有奇数项的和为165,所有偶数项的和为150,则n等于( B )
A.9 B.10 C.11 D.12
1. 在等差数列{an}中,已知S15=90,那么a8等于( C )
A.3 B.4 C.6 D.12
6.在等差数列{an}中,an=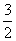 n-
n-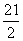 ,当n为何值时,前n项和Sn取得最小值?
,当n为何值时,前n项和Sn取得最小值?
 [解法一] 由
[解法一] 由 可解得6≤n≤7,可知前6项都是正数,第7项为0,因此S6=S7为Sn的最小值.
可解得6≤n≤7,可知前6项都是正数,第7项为0,因此S6=S7为Sn的最小值.
[解法二] 由an=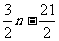 知Sn=a1+a2+…+an=
知Sn=a1+a2+…+an=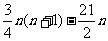 =
=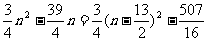
∴当n=6或n=7时,Sn取得最小值.
[选修延伸]
[例5] 已知数列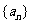 的前
的前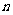 项和
项和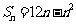 ,求数列
,求数列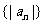 的前
的前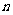 项和
项和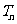 。
。
分析 :由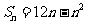 知
知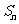 是关于
是关于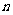 的无常数项的二次函数(
的无常数项的二次函数(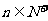 ),可知
),可知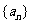 为等差数列,可求出
为等差数列,可求出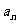 ,然后再判断哪些项为正,那些项为负,求出
,然后再判断哪些项为正,那些项为负,求出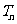 。
。
[解]当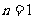 时,
时,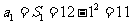 ;
;
当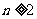 ,
,
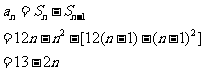 。
。
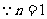 时适合上式,
时适合上式,
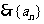 的通项公式为
的通项公式为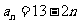 。
。
由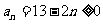 ,得
,得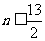 ,
,
即当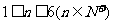 时,
时,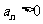 ;
;
当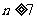 时,
时,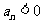 。
。
(1)当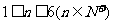 时,
时,
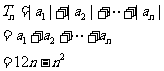
(2)当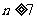
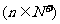 时,
时,
 .
.
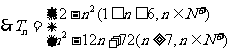 。
。
[追踪训练二]
5.在等差数列{an}中,已知前4项和是1,前8项和是4,则a17+a18+a19+a20等于___9__.
4.在等差数列{an}中,已知a14+a15+a17+a18=82,则S31=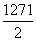 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com