
5.等比数列中,首项为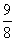 ,末项为
,末项为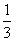 ,公比为
,公比为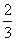 ,则项数
,则项数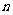 等于
.
等于
.
4. 等差数列{an}中,an-m = A,an+m =B.等比数列{bn}中,bn-m = A,bn+m =B.则有( )
A.an =A + B,bn =A·B
B.an
=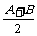 ,bn =
,bn =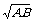
C.an
=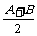 ,bn =±
,bn =±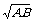
D.a2n =A + B,b2n =AB
3. 考察下列数列,①a1 =1,an+1 =an + 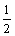 ,b1 =2,bn+1 =bn·2.
②an+1 =an
,bn+1 =2bn. ③an+1 =an+n,b1 =1,bn+1 =(bn)2 ,则{an}是等差数列且{bn}是等比数列的有( )
,b1 =2,bn+1 =bn·2.
②an+1 =an
,bn+1 =2bn. ③an+1 =an+n,b1 =1,bn+1 =(bn)2 ,则{an}是等差数列且{bn}是等比数列的有( )
A.1组 B.2组 C.3组 D.0组
2.等比数列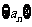 中,
中,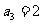 ,
,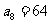 ,那么它的公比
,那么它的公比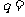 ( )
( )
A. 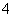 B.
B. 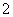 C.
C. 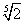 D.
D. 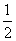
1.下列各组数能组成等比数列的是( )
A. 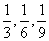 B.
B. 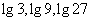
C. 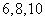 D.
D. 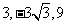
24、(I)证明: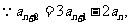
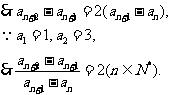
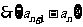 是以
是以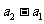
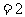 为首项,2为公比的等比数列。
为首项,2为公比的等比数列。
(II)解:由(I)得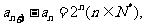

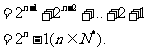
(III)证明: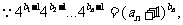
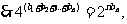
 ①
①
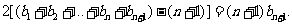 ②
②
②-①,得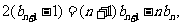
即 ③
③
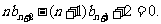 ④
④
④-③,得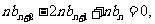
即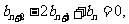
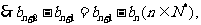
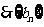 是等差数列。
是等差数列。
23、解: ∵10Sn=an2+5an+6, ① ∴10a1=a12+5a1+6,解之得a1=2或a1=3.
又10Sn-1=an-12+5an-1+6(n≥2),②
由①-②得 10an=(an2-an-12)+6(an-an-1),即(an+an-1)(an-an-1-5)=0
∵an+an-1>0 , ∴an-an-1=5 (n≥2).
当a1=3时,a3=13,a15=73. a1, a3,a15不成等比数列∴a1≠3;
当a1=2时, a3=12, a15=72, 有 a32=a1a15 , ∴a1=2, ∴an=5n-3.
21、2
22、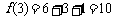 ;观察图4,不难发现第
;观察图4,不难发现第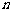 堆最底层(第一层)的乒乓球数
堆最底层(第一层)的乒乓球数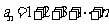
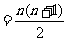 ,第
,第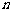 堆的乒乓球总数相当于
堆的乒乓球总数相当于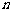 堆乒乓球的底层数之和,即
堆乒乓球的底层数之和,即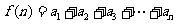
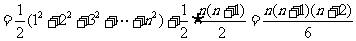
20、54
13、A 14、B 15、D 16、C 17、B 18、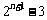 19、
19、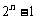
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com