
9.解:设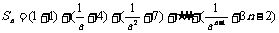 将其每一项拆开再重新组合得
将其每一项拆开再重新组合得
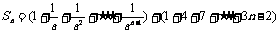 (分组)
(分组)
当a=1时,
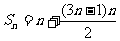 =
=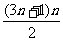 (分组求和)
(分组求和)
当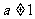 时,
时,
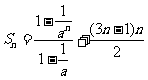
=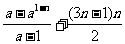
8.解: ∵ 
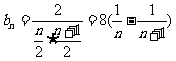
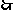 数列{bn}的前n项和:
数列{bn}的前n项和:
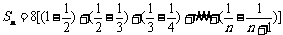 =
=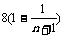 =
= 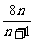
7. 8
6. 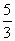
1.A 2.B 3.C 4.A 5.C
12.∵等比数列中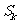 ,
,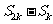 ,
,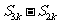 ,……仍成等比数列,∴
,……仍成等比数列,∴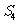 ,
, ,
,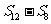 ,……也成等比数列,而
,……也成等比数列,而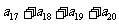 则是这个等比数列中的第5项,由
则是这个等比数列中的第5项,由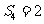 ,
,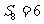 得
得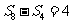 ∴这个等比数列即是:2,4,8,16,32,……,∴
∴这个等比数列即是:2,4,8,16,32,……,∴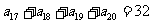 .
.
第13课时 等比数列的
前n项和(2)
11. 由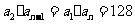 ,又
,又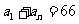 得,
得, 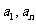 是方程
是方程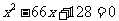 的两根,解这个方程得,
的两根,解这个方程得,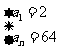 或
或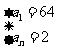 ,由
,由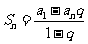 得
得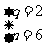 或
或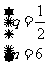 .
.
1.B 2.C 3.D 4.C 5.B 6.D 7.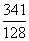 8.
8.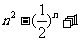 9.27 10.
9.27 10.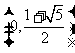
10. 解:(1)an+1 = Sn+1 –Sn
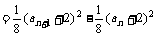 ,
,
∴8 an+1
=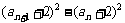 ,
,
∴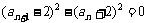 ,
,
∴(an+1 + an)(a n+1 – a n – 4)=0,
∵an∈N*,∴an+1 + an≠0,
∴a n+1 – a n – 4=0,即a n+1 – a n = 4,
∴数列{an}是等差数列.
(2)由a n+1 – a n = 4,由题知
Bn+1 = 5Bn – 4 Bn–1
Bn+1 – Bn = 4(Bn – Bn–1)
bn+1 = 4bn(n≥2)
又已知b1 = 1,b2 = 4.
故{bn}是首项为1,公比为4的等比数列.
an =4n –1 (n∈N+)
第12课时 等比数列的
前n项和(1)
9.∵在等比数列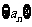 中,
中, 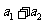 ,
,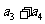 ,
,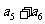 也成等比数列,∵
也成等比数列,∵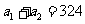 ,
,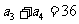 ∴
∴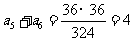
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com