2．例2是常见典型错误，它违背了最值定理使用前提：“一正二定三相等”中的后两条。

追踪训练一

1．利用基本不等式求最值问题时，一定要交代等号何时成立，只有等号成立了，才能求最值，否则要用其它方法了．而在证明不等式时，不必要交代等号何时成立．

2．最值定理中隐含三个条件：　　　

　　　　　　　　．

[精典范例]

例1．(1).已知函数y=x+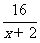(x>－2), 求此函数的最小值.

(2)已知x<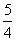, 求y=4x－1+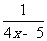的最大值;

(3)已知x>0 , y>0 , 且5x+7y=20 , 求xy的最大值;

(4)已知x , y∈R⁺ 且x+2y=1 , 求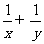的最小值.

[解]

例2. 错在哪里?

(1)求y=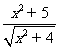(x∈R)的最小值.

解∵y=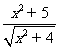

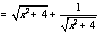
∴ y的最小值为2 .

.(2)已知x , y∈R⁺ 且x+4y=1，求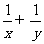

　的最小值．

法一：由1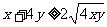＝得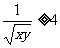

所以．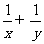

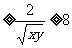所以原式最小值为8．

法二：由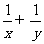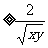(当且仅当x=y时等号成立)．于是有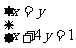得x=y=0.2．所以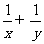的最小值为5+5=10.

思维点拔：

1．最值定理：

若x、y都是正数，

(1)如果积xy是定值P , 那么当且仅当x=y时, 和x+y有最小值　　　．.

(2)如果和x+y是定值S , 那么当且仅当x=y时, 积xy有最大值　　　．

2. 运用基本不等式求解函数最值问题．

[课堂互动]

自学评价

1. 理解最值定理的使用条件：

一正二定三相等．

3．已知a+b+c=1,求证a²+b²+c²≥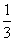

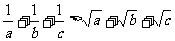2．已知a>1求证a+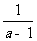≥3

1．设P为正数，求下列各组数的算术平均数与几何平均数．

(1)2与8

(2)3与12

(3)P与9P

(4)2与2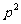

2．基本不等式的推广：n个(n>1)非负数的几何平均数不大于它们的算术平均数．即若a_i≥0(i=1,2,…,n),则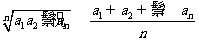(n>1,n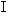N)

追踪训练